Força centrífuga

A força centrífuga é uma força imaginária que atua em um corpo no sentido oposto à força centrípeta. Considerando-a uma força real, seu conceito é utilizado quando o objetivo é separar alguma mistura rotacionando-a.

Enquanto a força centrípeta possui o sentido para o centro do movimento circular, a força centrífuga tem sentido para fora do círculo descrito no movimento, porém a verdade é que isso ocorre pela ação da primeira lei de Newton. Como, em teoria, as forças centrífuga e centrípeta são iguais, mas com sentidos opostos, são também calculadas da mesma forma.

Leia também: Força normal — a força que uma superfície exerce sobre um objeto

Tópicos deste artigo

• 1 - Resumo sobre força centrífuga
• 2 - O que é força centrífuga?
• 3 - Exemplos de força centrífuga
• 4 - Como calcular a força centrífuga?
• 5 - Diferenças entre força centrífuga e força centrípeta
• 6 - Exercícios resolvidos sobre força centrífuga

Resumo sobre força centrífuga

• A força centrífuga é fictícia e seu resultado é desvincular um corpo do movimento circular que ele está executando.

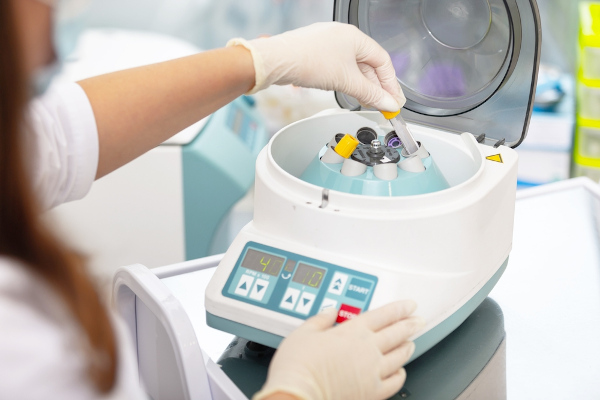
• São um exemplo dela as centrífugas utilizadas em exames laboratoriais.

• A força centrífuga pode ser calculada pela seguinte fórmula:

\(F_{centrífuga}=\frac{m\cdot v²}R \)

• Em termos da velocidade angular ω, a fórmula é a seguinte:

\(F_{centrífuga}=m\cdotω^2\cdot R\)

• A força centrípeta difere da força centrífuga no sentido, sendo que a centrípeta exerce sentido para o centro do círculo que o movimento executa e a centrífuga tem seu sentido na direção oposta.

O que é força centrífuga?

A centrífuga é uma força imaginária que tem a capacidade de distanciar um corpo que está descrevendo uma trajetória circular do centro do círculo descrito por ele, logo, a centrífuga implica “fuga do centro”. Por se tratar de uma força, sua unidade de medida é o newton N.

A força centrífuga é “fictícia” por três motivos, que inclusive fazem com que ela seja considerada também uma força inercial, que são os seguintes:

• Primeiro motivo: ela só ocorre quando o movimento circular está ocorrendo, ou seja, se o corpo estiver em repouso, ela não age, e, como a velocidade do corpo está variando constantemente, o corpo não entra em equilíbrio.

• Segundo motivo: caso houvesse uma força com o sentido oposto ao centro da circunferência e outra no sentido do centro (centrípeta), ambas se anulariam e o movimento deixaria de ser circular, tornando-se retilíneo.

• Terceiro motivo: o corpo não é expulso da trajetória circular, o que ocorre na realidade é a primeira lei de Newton (princípio da inércia). Por exemplo, quando dois corpos se movem simultaneamente no movimento circular, a velocidade que atua é a linear, a rotação é devido à aceleração centrípeta, sendo assim, se um corpo se desvincular do movimento, ele manterá o sentido dessa velocidade, logo, uma linha reta. Isso é visível quando se está dentro de um veículo em movimento e ele faz uma curva, fazendo com que os passageiros e motorista tenham a impressão de se inclinar para o lado oposto da curva, quando na verdade seus corpos tendem a continuar em linha reta.

Exemplos de força centrífuga

A força centrífuga, embora fictícia, tem seu conceito amplamente utilizado. Veja, a seguir, alguns exemplos:

• Aparelho laboratorial centrífuga: na medicina, geralmente é utilizado para separação dos componentes do sangue. Ele separa de misturas por meio do movimento circular com altas velocidades.

• Função de centrifugação das máquinas de lavar roupa: nessa função a roupa descreve o movimento circular executado pelo cesto da máquina, que contêm vários furos e no qual a roupa é separada da água.

• Arma de arremesso funda: consiste em girar uma pedra em um pedaço de corda, para fazer com que ela adquira velocidade e, com isso, atinja o alvo com mais força. Tal arma ficou famosa devido à história bíblica cristã de Davi e Golias, no entanto, ela é ainda amplamente utilizada, por exemplo, por algumas tribos indígenas.

Como calcular a força centrífuga?

A força centrífuga é calculada pela mesma fórmula da força centrípeta, que equivale ao produto da massa m (medida em quilogramas kg) do corpo que executa o movimento circular pela razão entre a velocidade linear v (medida em metros por segundos m/s) elevada ao quadrado e o raio R (medido em metros) da circunferência formada.

\(F_{centrífuga}=\frac{m\cdot v²}R \)

Em termos da velocidade angular (ω), a equação anterior pode ser reescrita da forma a seguir.

\(F_{centrífuga}=m\cdotω^2\cdot R\)

Exemplo:

Uma criança está rodando um brinquedo de 3 kg que está preso na extremidade de uma corda de 0,6 m de comprimento segurando a outra extremidade da corda. Quando ela solta o brinquedo, ele atinge uma velocidade de 8 m/s. Qual seria o valor da força centrífuga nesse sistema?

Resolução:

Extraindo os dados do problema:

R = 0,6 m

m = 3 kg

v = 8 m/s

F_centrífuga = ?

\(F_{centrífuga}=m\cdot \frac{v^2}R=3\cdot\frac{8^2}{0,6}=3\cdot\frac{64}{0,6}=\frac{192}{0,6}\)

\(F_{centrífuga}=320\ N\)

Diferenças entre força centrífuga e força centrípeta

A força centrífuga é uma força fictícia cujo sentido é oposto ao centro da circunferência formada pelo movimento. Por sua vez, a força centrípeta é uma força real e seu sentido é para o centro da circunferência.

Ao contrário do que é pensado, ambas não atuam no mesmo corpo, porque, caso o fizessem, seriam anuladas e o corpo descreveria um trajeto retilíneo. Essas duas forças não são um par de ação e reação, conforme muitas vezes se acredita, e isso está errado devido justamente ao fato de não atuarem sobre um mesmo corpo.

Saiba mais: Aplicações da força centrípeta em lombadas e depressões

Exercícios resolvidos sobre força centrífuga

Questão 1

Teodoro confeccionou uma funda que, dobrada com a corda, media 40 centímetros. A pedra tinha 0,2 kg, e, após rotacionar a funda, segurando na sua extremidade, Teodoro lançou a pedra com uma força de 72 N. Marque a alternativa que representa a velocidade com a qual a pedra foi lançada.

A) 9 m/s

B) 12 m/s

C) 20 m/s

D) 5 m/s

E) 10 m/s

Resolução:

Alternativa B

Extraindo os dados do problema:

F_centrífuga = 72 N

R = 40 cm

m = 0,2 kg

v = ?

Incialmente é necessário converter o raio de centímetros para metros, dividindo o valor por 100.

\(R=\frac{40\ cm}{100}=0,4 m\)

\(F_{centrífuga}=\frac{m\cdot v²}R \)

\(72=0,2\cdot \frac{v^2}{0,4}\)

O 0,4 passará multiplicando o 72.

\(72\cdot0,4=0,2\cdot v^2\)

Invertendo ambos os lados da equação:

\(0,2\cdot v^2=72\cdot0,4\)

\(v^2=\frac{28,8}{0,2}=144\)

\(v^2=144\)

Como a variável está elevada ao quadrado, acrescenta-se raiz quadrada em ambos os lados da equação para eliminar o expoente.

\(\sqrt{v^2}=\sqrt{144}\)

\(v=12\ m/s\)

Questão 2

Para um teste de qualidade de um novo elástico, em um laboratório de física foi utilizado 0,9 m do elástico em questão. Em uma de suas extremidades, foi fixado um objeto de 2 kg, e a outra extremidade foi presa a uma máquina que rotacionou o elástico e parou de imediato quando o giro atingiu a velocidade angular igual a 6 rad/s, e, com isso, o elástico sofreu uma deformação de 0,4 m. O valor da constante elástica que constará nas especificações do elástico será:

A) 520 N/m

B) 811 N/m

C) 633 N/m

D) 162 N/m

E) 20 N/m

Resolução:

Alternativa D

Extraindo os dados do problema:

R = 0,9 m

m = 2 kg

ω = 6 rad/s

x = 0,4 m

K = ?

Para o que foi descrito no problema ser possível, a força elástica deverá ser igual à força centrífuga em termos de velocidade angular.

\(F_{elática}=F_{centrífuga}\)

Força elástica é igual ao produto entre deformação do elástico e a constante elástica K.

\(F_{elática}=K\cdot x\)

\(F_{elática}=F_{centrífuga}\)

\(K\cdot x=m\cdot ω^2\cdot R\)

\(K\cdot04=2\cdot6^2\cdot0,9\)

\(K\cdot04=2\cdot36\cdot0,9\)

\(K\cdot04=64,8\)

\(K=\frac{64,8}{0,4}=162\ N/m\)

Por Gustavo Campos
Professor de Física