Torque, ou momento de uma força, é a tendência que uma força tem de rotacionar um corpo sobre o qual ela é aplicada. O torque é um vetor perpendicular ao plano formado pelos vetores força e raio de rotação. O vetor torque pode ser calculado por meio do produto vetorial entre força e distância.
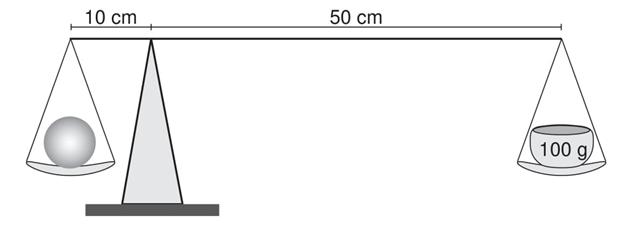
Sempre que uma força for aplicada a alguma distância do eixo de rotação de um corpo, esse corpo estará sujeito à rotação. Se esse corpo não está rotacionando ou rotaciona com velocidade angular constante, dizemos que ele se encontra em equilíbrio rotacional. O equilíbrio rotacional indica que a resultante dos torques que atuam sobre um corpo é nula e, por isso, esse corpo rotaciona com velocidade constante ou nula. Em outras palavras, quando o torque resultante sobre um corpo é nulo, esse corpo não apresenta aceleração angular.
O torque pode ser entendido como o agente dinâmico das rotações. Dessa forma, ele está para os movimentos de rotação, assim como a força está para os movimentos de translação. Se quisermos fazer que um corpo gire em torno de algum ponto, devemos exercer um torque sobre ele.
Tópicos deste artigo
- 1 - Unidade de torque
- 2 - Fórmula
- 3 - Torque e momento angular
- 4 - Exemplos de torque
- 5 - Exercícios resolvidos sobre torque
Unidade de torque
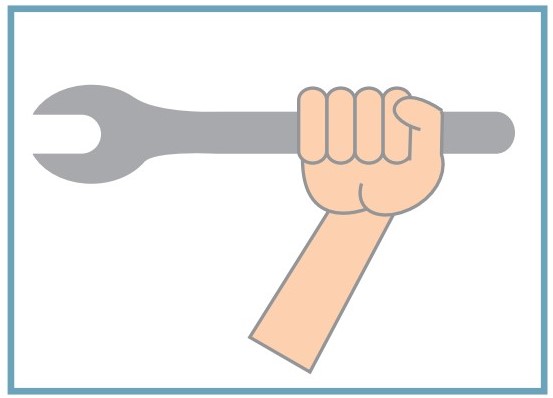
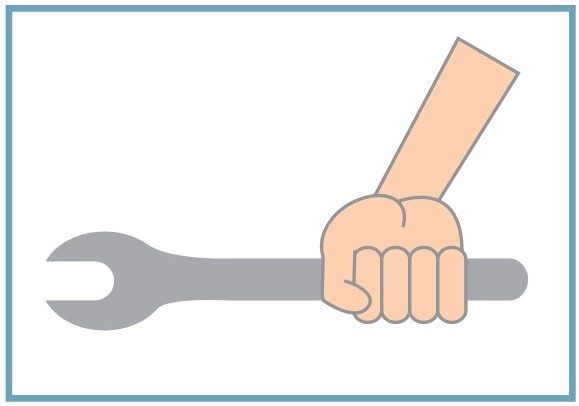
A unidade do torque, de acordo com o Sistema Internacional, é o Newton vezes metro (N.m). Por definição, quando um corpo é rotacionado no sentido horário, seu torque é negativo; no caso contrário, o torque aplicado sobre ele tem módulo positivo. Além disso, a direção e o sentido do vetor torque podem ser facilmente determinados por meio da regra da mão direita. Confira o esquema a seguir:
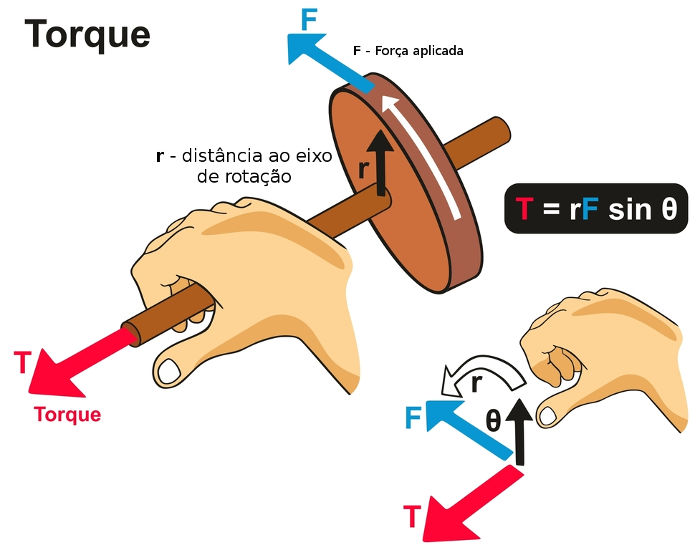
O torque pode ser determinado fechando a mão em direção à força (F). Ele é determinado pela direção do dedão.
Fórmula
O módulo do torque pode ser calculado pelo produto da força, distância e pelo seno do ângulo que é formado entre essas duas grandezas:
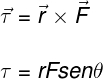
τ – torque
r – raio
F – força
θ – ângulo entre r e F
Na fórmula acima, θ é o ângulo formado entre o raio de rotação (r) e a força (F). No caso em que a força é aplicada com um ângulo de 90º em relação ao raio (r), o seno do ângulo é igual a 1. O raio (r) é determinado pela distância do ponto de aplicação até o eixo de rotação do corpo e também é conhecido como braço de alavanca. Quanto maior for o braço de alavanca de um corpo, mais fácil será rotacioná-lo.
Torque e momento angular
O torque é o agente dinâmico da rotação. Quando aplicamos um torque sobre algum corpo, esse corpo pode ganhar velocidade angular, passando a descrever um movimento de rotação. Dizemos que, quando um corpo está em rotação, ele apresenta momento angular. O momento angular é o análogo rotacional do momento linear, também conhecido como quantidade de movimento, por isso, podemos entender que o momento angular é a quantidade de movimento rotacional de um corpo ou sistema.
Quando o torque resultante sobre um corpo é nulo, o seu momento angular permanece constante, caso contrário, o momento angular seria alterado.
De forma similar à força, que pode ser escrita como a variação temporal da quantidade de movimento, o torque pode ser entendido como a variação da quantidade de movimento angular em relação ao tempo.
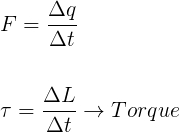
O momento angular, por sua vez, pode ser calculado pelo produto vetorial da posição do corpo com a sua quantidade de movimento. O módulo do momento angular de um corpo em rotação é determinado por:

L – momento angular (kg.m²/s)
r – raio da trajetória (m)
Q – quantidade de movimento (kg.m/s)
θ – ângulo entre r e Q
Exemplos de torque
-
Quando abrimos uma porta, aplicamos força em um ponto distante do seu eixo de rotação, dessa forma, imprimimos sobre ela um torque maior.
Anuncie aqui -
Quando pedalamos em uma bicicleta de marchas, é possível notar que, quanto maior for o diâmetro de sua coroa, maior será o torque produzido por cada pedalada.
-
Ao usarmos uma chave de fenda, é possível perceber que, quanto maior for o diâmetro do seu cabo, maior será a facilidade em apertar ou remover parafusos.
Exercícios resolvidos sobre torque
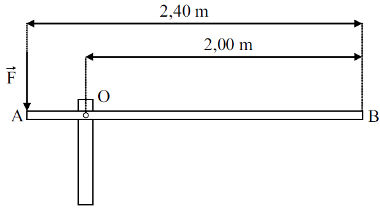
1) Uma força de 50 N é aplicada com ângulo de 45º em relação a um braço de alavanca de 0,25 m, fazendo uma manivela girar no sentido anti-horário.
Dados: sen 45º = √2/2
a) Determine a direção e o sentido do torque exercido sobre a manivela.
b) Calcule o torque realizado sobre a manivela.
Resolução
a) De acordo com a regra da mão direita, o torque está na direção perpendicular ao plano da maçaneta, e seu sentido aponta em direção ao plano da porta.
b) Usando a fórmula de torque e os dados do exercício, vamos fazer o seguinte cálculo:

2) Um torque de 100 N.m é aplicado a uma distância de 25 cm do eixo de rotação de um corpo. Determine a intensidade da força perpendicular ao plano de rotação desse corpo e calcule a variação de momento angular sofrida por esse corpo em um intervalo de tempo de 3 s.
Resolução
Para calcularmos a intensidade da força perpendicular ao eixo de rotação, vamos utilizar a definição de torque e os dados do exercício:
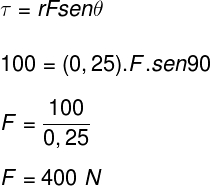
Para determinarmos a variação do momento angular sofrida por esse corpo, vamos fazer o cálculo a seguir:
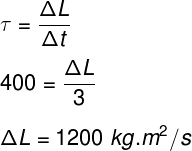
Por Me. Rafael Helerbrock