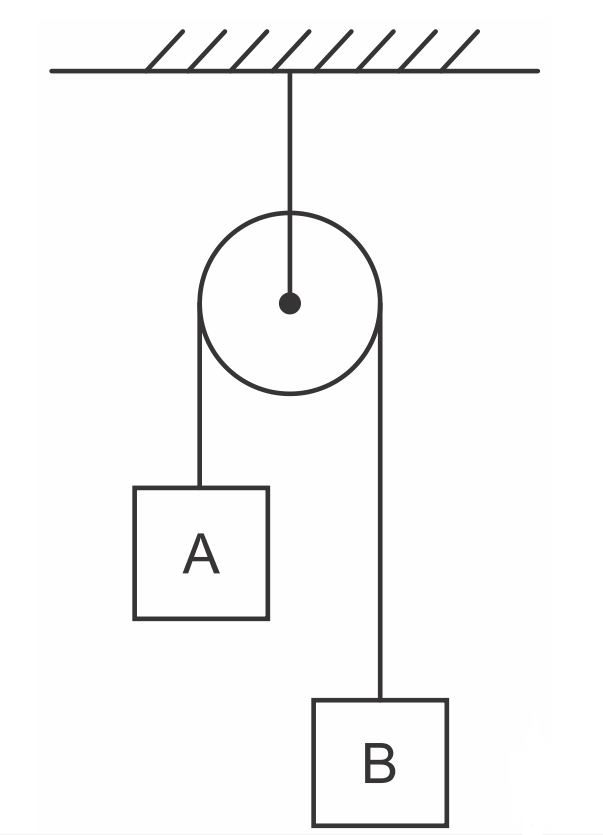
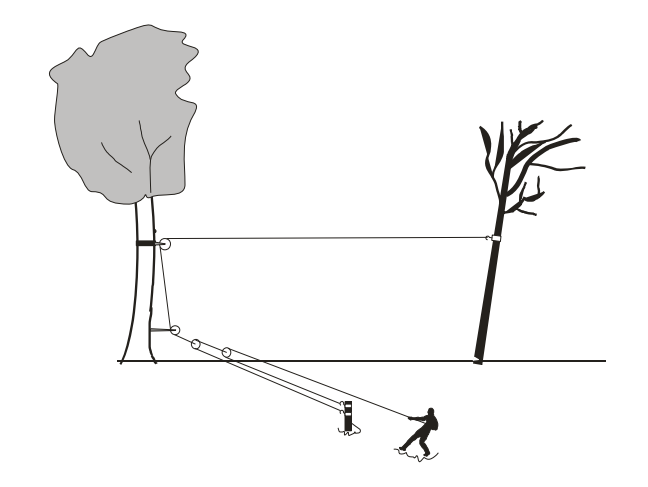
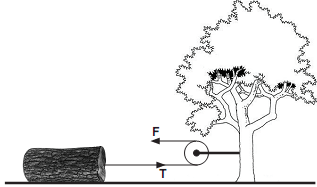
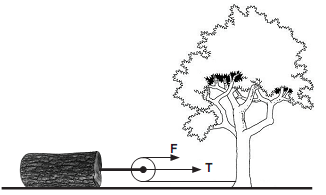
As roldanas, também conhecidas como polias, são peças mecânicas em que há um fio ligado a uma ou várias rodas fixas ou móveis que conectam um corpo a algo que realiza força sobre esse corpo. Elas são empregadas nas situações em que se deseja alterar a posição de um corpo.
Leia também: Alavancas — instrumentos que multiplicam a força aplicada sobre um corpo
Tópicos deste artigo
- 1 - Resumo sobre roldanas ou polias
- 2 - Videoaula sobre roldanas ou polias
- 3 - Função das roldanas
- 4 - Como funciona as roldanas?
- 5 - Tipos de roldanas
- 6 - Associação de roldanas móveis
- 7 - Uso de roldanas no cotidiano
- 8 - Mapa Mental: Roldanas
- 9 - Exercícios sobre roldanas ou polias
Resumo sobre roldanas ou polias
- As roldanas são um sistema composto por discos fixos ou móveis atrelados a um suporte que desloca um corpo.
- Propiciam o levantamento, abaixamento e deslocamento dos corpos de forma simples.
- Executam o seu movimento a partir das três leis de Newton.
- Podem ser fixas, quando têm o eixo preso a uma estrutura, ou móveis, quando têm o eixo livre, podendo se movimentar.
- A associação de roldanas móveis ocorre quando conectamos uma ou mais roldanas móveis a pelo menos uma roldana fixa.
- As roldanas são empregadas, por exemplo, nos guindastes, elevadores, poços artesianos, varais, equipamentos de escalada e muito mais.
Videoaula sobre roldanas ou polias
Função das roldanas
A função das roldanas é a de facilitar a elevação, descensão ou transporte de um corpo, o que dificilmente seria possível apenas com a ação humana.
Como funciona as roldanas?
As roldanas funcionam a partir das três leis de Newton, que são o Princípio da Inércia, o Princípio Fundamental da Dinâmica e o Princípio da Ação e Reação, sendo que cada uma das leis descreve um aspecto da funcionalidade das roldanas, conforme descrito abaixo.
- Princípio da Inércia: esse princípio diz respeito à manutenção do repouso ou movimento retilíneo e uniforme dos corpos quando a força resultante sobre eles for nula. No caso das roldanas, temos que é necessária a aplicação de uma força para levantar o corpo, retirando-o do seu estado de repouso. Além disso, se soltarmos o corpo conectado à roldana, ele continuará o seu movimento de queda até encontrar um obstáculo que inflija uma força sobre ele.
- Princípio Fundamental da Dinâmica: esse princípio diz respeito ao movimento de um corpo quando se aplica uma força sobre ele. No caso das roldanas, o movimento do corpo está condicionado às forças atuantes sobre ele. Geralmente nesse sistema temos a força peso (dada pela ação da gravidade), a força de tração (dada pela ação do fio) e a força aplicada pela pessoa. Nessa situação, o movimento do corpo ocorre porque a força aplicada sobre o fio é igual ou muito menor do que a força peso atuando sobre ele.
- Princípio da Ação e Reação: determina que toda força de ação realizada sobre um corpo provoca uma força de reação por ele. No caso das roldanas, de modo resumido, a ação de puxar o fio provoca a reação de subida do corpo, e a ação de soltar o fio provoca a reação de descida do corpo.
Tipos de roldanas
Existem dois tipos de roldanas: as roldanas fixas e as roldanas móveis.
-
Roldanas fixas
As roldanas fixas são aquelas possuem um eixo fixado a um suporte, que pode ser o teto ou um poste. Ao empregar roldanas fixas é possível obter diversas vantagens, tais como elevar ou abaixar objetos a/de alturas elevadas, transportar objetos a longas distâncias, não modificar a força necessária para movimentar o objeto e preservar a saúde pela possibilidade de realizar o movimento de forma ereta.
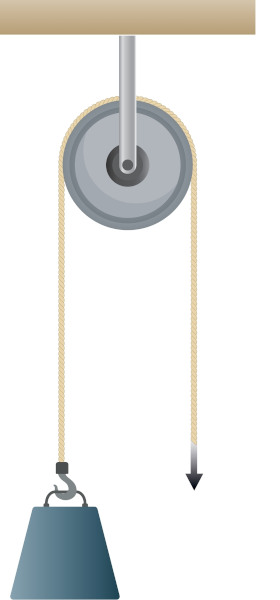
Veja um exemplo de exercício envolvendo a roldana fixa:
1. Qual a força necessária para elevar um bloco de 10 kg, sabendo que ele está associado a uma roldana fixa, conforme descrito na imagem abaixo? Considere a aceleração da gravidade como 10 m/s2.
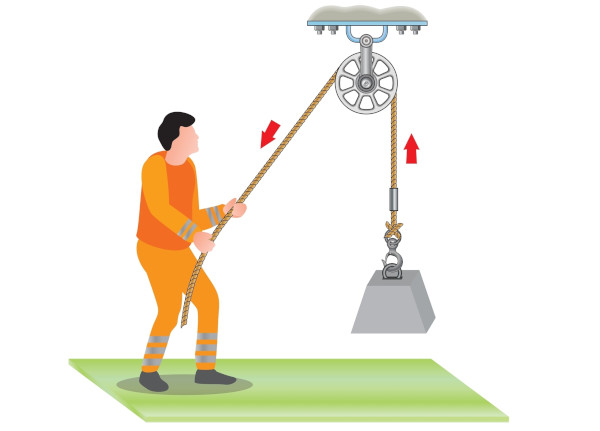
Resolução: Quando temos um corpo conectado a uma roldana fixa, a força necessária para deslocá-lo é igual à força peso sobre ele, então:
\(F=P\)
\(F=m\cdot g\)
\(F=10\cdot10\)
\(F=100\ N\)
-
Roldanas móveis
As roldanas móveis são aquelas que possuem o eixo livre, apresentando um movimento rotacional e translacional. Ao empregar roldanas móveis é possível reduzir a força necessária para movimentar um objeto, consequentemente havendo a redução do seu peso pela metade. Então, quanto mais roldanas móveis forem empregadas em um sistema, menos força precisará ser realizada para mover o objeto.
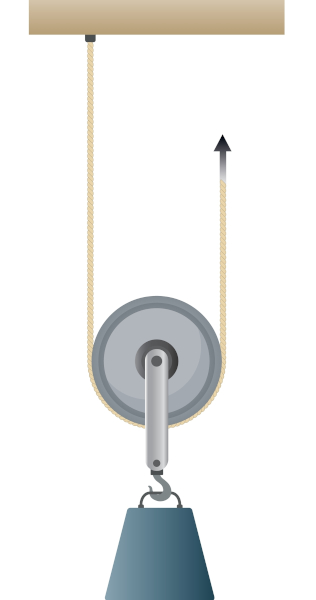
Veja um exemplo de exercício com roldanas móveis:
1. Qual a força necessária para puxar um haltere de 20 kg que está associado a uma roldana móvel conectada a uma roldana fixa, conforme descrito na imagem abaixo? Considere a aceleração da gravidade como 10 m/s2 .
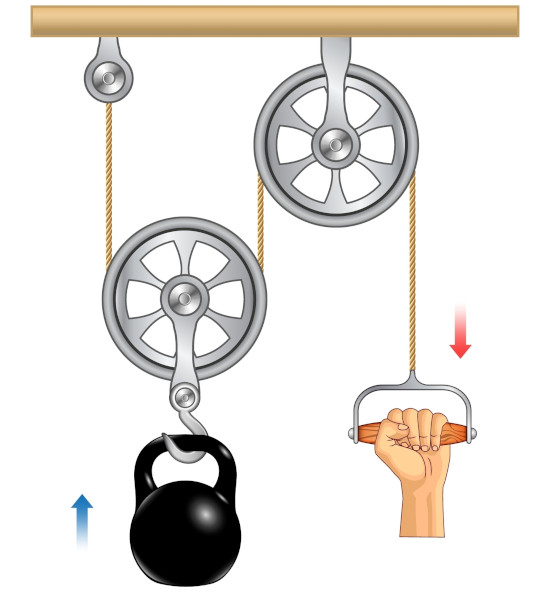
Resolução: Quando temos um corpo conectado a uma roldana fixa, a força necessária para deslocá-lo é igual à força peso sobre ele, então:
\(F=P\)
\(F=m\cdot g\)
\(F=20\cdot10\)
\(F=200\ N\)
Contudo, temos também uma roldana móvel conectada à roldana fixa. A força necessária para deslocar o corpo é dada pela fórmula:
\(F=\frac{P}{2^n}\)
\(F=\frac{200}{2^1}\)
\(F=\frac{200}{2}\)
\(F=100\ N\)
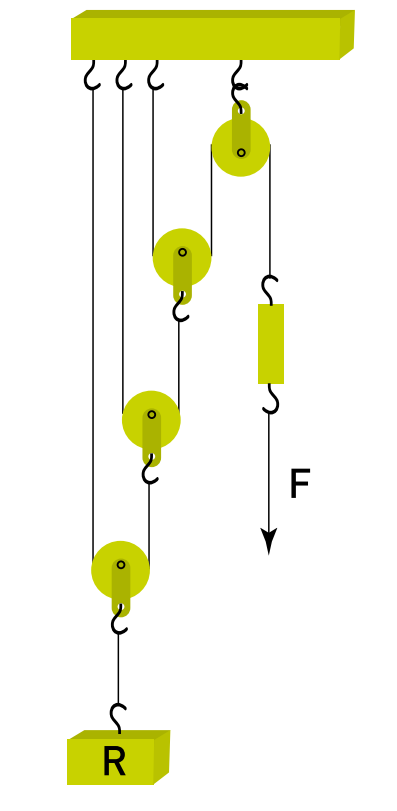
Associação de roldanas móveis
A associação de roldanas móveis é empregada com o intuito de minimizar a força necessária para movimentar um objeto. Conecta-se no mínimo uma roldana móvel a uma roldana fixa, como descrito na imagem abaixo:
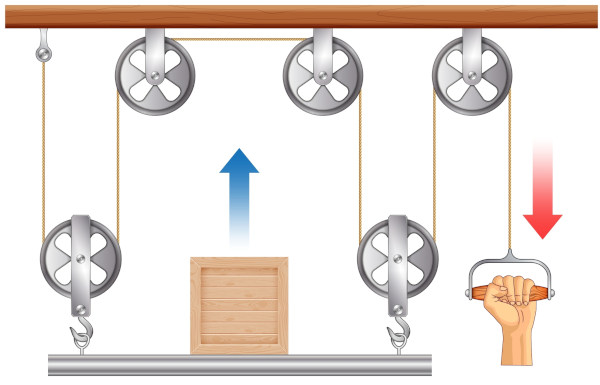
A fórmula que rege a associação de roldanas móveis é dada por
\(F=\frac{P}{2^n}\)
- F é a força necessária para mover o objeto, medida em Newton .
- P é a força peso, medida em Newton .
- n é a quantidade de roldanas móveis associadas ao sistema.
Leia também: Como calcular o trabalho de uma força
Uso de roldanas no cotidiano
As roldanas são amplamente usadas no cotidiano, em vista disso selecionamos abaixo alguns exemplos de usos das roldanas:
- guindastes;
- elevadores;
- poços artesianos;
- equipamentos de escalada;
- equipamentos de academia;
- varais;
- sistemas de guincho;
- sistemas de içar bandeiras e velas dos barcos.
Mapa Mental: Roldanas
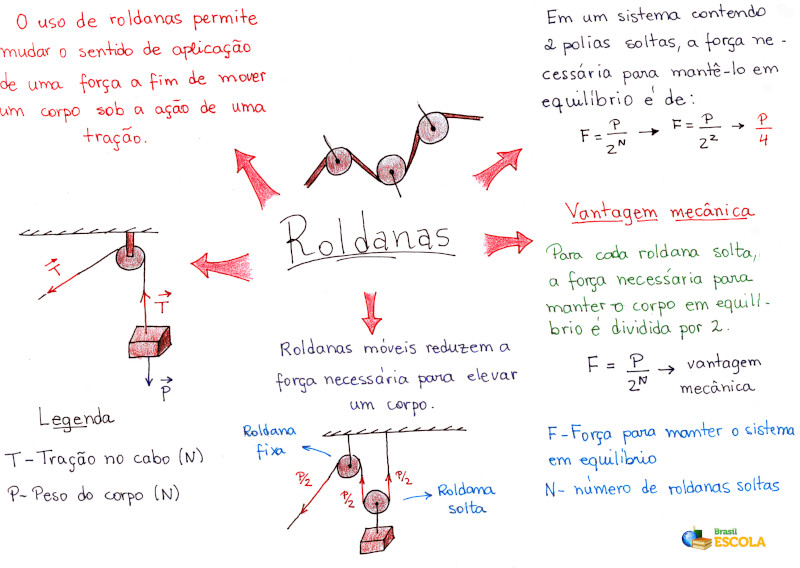
* Baixe o mapa mental sobre roldanas!
Exercícios sobre roldanas ou polias
Questão 1
(Cesgranrio-RJ) Um corpo de peso P encontra-se em equilíbrio devido à ação da força de intensidade F aplicada pela moça da figura abaixo.
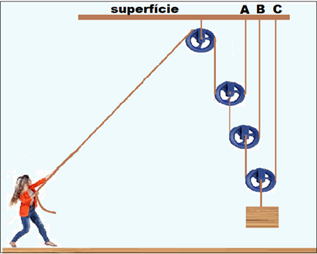
Os pontos A, B e C são os pontos de contato entre os fios e a superfície. A força que a superfície exerce sobre os fios nos pontos A, B e C são, respectivamente,
a) \(\frac{P}{8}, \frac{P}{4},\ \frac{P}{2}\)
b) \(\frac{P}{8}, \frac{P}{2},\ \frac{P}{4}\)
c) \(\frac{P}{2}, \frac{P}{4},\ \frac{P}{8}\)
d) \(P, \frac{P}{2},\ \frac{P}{4}\)
e) iguais a P
Resolução:
Alternativa A. Calcularemos a força que a superfície exerce sobre os fios nos pontos A, B e C através da fórmula da associação de roldanas móveis:
\(F=\frac{P}{2^n}\)
No ponto A, temos três roldanas móveis associadas, então:
\(F=\frac{P}{2^n}\)
\(F=\frac{P}{2^3}\)
\(F=\frac{P}{8}\)
No ponto B, temos duas roldanas móveis associadas, então:
\(F=\frac{P}{2^n}\)
\(F=\frac{P}{2^2}\)
\(F=\frac{P}{4}\)
No ponto C, temos uma roldana móvel associada, então:
\(F=\frac{P}{2^n}\)
\(F=\frac{P}{2^1}\)
\(F=\frac{P}{2}\)
Questão 2
(UFU-MG – adaptada) Na figura abaixo despreze as forças dissipativas e calcule o valor da carga Q, sabendo que o rapaz exerce uma força de 25 N para mantê-la em equilíbrio.
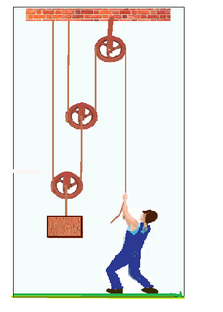
a) 100 N
b) 200 N
c) 300 N
d) 400 N
e) 500 N
Resolução:
Alternativa A. Calcularemos o valor da carga Q, representada pela força peso, através da fórmula da associação de roldanas móveis:
\(F=\frac{P}{2^n}\)
\(25=\frac{P}{2^2}\)
\(25=\frac{P}{4}\)
\(P=25\cdot4\)
\(P=100\ N\)
Fontes:
NUSSENZVEIG, Herch Moysés. Curso de física básica: Mecânica (vol. 1). 5 ed. São Paulo: Editora Blucher, 2015.
HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Mecânica. 8. ed. Rio de Janeiro, RJ: LTC, 2009.