A energia potencial elástica é um tipo de energia potencial ligada às propriedades elásticas dos materiais, cuja compressão ou elasticação é capaz de produzir o movimento dos corpos. Sua unidade de medida é o Joule, e ela pode ser calculada pelo produto entre a constante elástica e o quadrado da deformação sofrida pelo objeto elástico, dividido por dois.
Tópicos deste artigo
- 1 - Resumo sobre energia potencial elástica
- 2 - O que é energia potencial elástica?
- 3 - Fórmulas da energia potencial elástica
- 4 - Aplicações da energia potencial elástica
- 5 - Transformação da energia potencial elástica
- 6 - Vantagem e desvantagem da energia potencial elástica
- 7 - Diferenças entre energia potencial elástica e energia potencial gravitacional
- 8 - Exercícios resolvidos sobre energia potencial elástica
Resumo sobre energia potencial elástica
-
A energia potencial elástica é uma forma de energia potencial associada à deformação e à alongação de corpos elásticos.
-
Sua fórmula de cálculo é a seguinte:
\(E_{pel}=\frac{k\cdot x^2}2\)
-
Também pode ser calculada pela fórmula que relaciona a energia potencial elástica à força elástica:
\(E_{pel}=\frac{F_{pel}\cdot x}2\)
-
Na física, a energia sempre é conservada, nunca gerada ou destruída.
-
É possível transformarmos a energia potencial elástica em energia potencial gravitacional e/ou em energia cinética.
-
A energia potencial elástica se converte em energia cinética mais lentamente do que a energia potencial gravitacional se converteria.
-
A energia potencial gravitacional está relacionada à variação de altura dos corpos localizados em uma região com campo gravitacional.
O que é energia potencial elástica?
A energia potencial elástica é uma grandeza física escalar relacionada à ação produzida por materiais elásticos ou flexíveis sobre outros corpos. São exemplos de materiais elásticos ou flexíveis as molas, as borrachas, os elásticos. Ela é uma das formas de energia potencial, assim como a energia potencial gravitacional.
De acordo com o Sistema Internacional de Unidades (SI), sua unidade de medida é o Joule, representado pela letra J.
Ela é diretamente proporcional à constante elástica e à deformação sofrida pelos objetos elásticos, portanto, à medida que elas aumentam, a energia potencial elástica também aumenta.
Fórmulas da energia potencial elástica
→ Energia potencial elástica
\(E_{pel}=\frac{k\cdot x^2}2\)
-
\(E_{pel}\) → energia potencial elástica, medida em Joule \(\).
-
k → constante elástica, medida em Newton por metro \([N/m]\).
-
x → deformação do objeto, medida em metros\(\).
Exemplo:
Determine a energia potencial elástica em uma mola que sofre uma deformação de 0,5 m sabendo que sua constante elástica é de 200 N/m.
Resolução:
Calcularemos a energia potencial elástica por meio da sua fórmula:
\(E_{pel}=\frac{k\cdot x^2}2\)
\(E_{pel}=\frac{200\cdot 0,5^2}2\)
\(E_{pel}=\frac{200\cdot 0,25}2\)
\(E_{pel}=25\ J\)
A energia potencial elástica é de 25 Joules.
→ Energia potencial elástica relacionada à força elástica
\(E_{pel}=\frac{F_{pel}\cdot x}2\)
-
\(E_{pel}\) → energia potencial elástica, medida em Joule \(\).
-
\(F_{el}\) → força elástica, ou seja, a força exercida pela mola, medida em Newton \( \).
-
x → deformação do objeto, medida em metros \(\).
Não pare agora... Tem mais depois da publicidade ;)
Exemplo:
Qual a energia potencial elástica em uma mola que sofre uma deformação de 2,0 cm quando submetida à ação de uma força de 100 N?
Resolução:
Primeiramente converteremos a deformação de centímetros em metros:
20 cm = 0,2 m
Então calcularemos a energia potencial elástica pela fórmula que a relaciona à força elástica:
\(E_{pel}=\frac{F_{pel}\cdot x}2\)
\(E_{pel}=\frac{100\cdot0,2}2\)
\(E_{pel}=10\ J\)
A energia potencial elástica é de 10 Joules.
Aplicações da energia potencial elástica
As aplicações da energia potencial elástica se referem principalmente a sua transformação em outras formas de energia ou ao armazenamento da energia cinética. Abaixo veremos alguns exemplos cotidianos das suas aplicações.
-
Os para-choques dos automóveis são desenvolvidos para se deformarem quando sofrem um impacto, armazenando o máximo de energia cinética e convertendo-a em energia potencial elástica.
Não pare agora... Tem mais depois da publicidade ;) -
Na cama elástica, temos a deformação das molas e do material elástico, provocando uma energia potencial elástica que, posteriormente, será convertida em energia cinética e energia potencial gravitacional.
-
Alguns tênis possuem molas que diminuem o impacto sofrido pelo movimento, em que a energia cinética está se transformando em energia potencial elástica.
Transformação da energia potencial elástica
A energia potencial elástica obedece ao princípio de conservação da energia, em que a energia é sempre conservada, não podendo ser criada nem destruída. Devido a isso, ela pode ser convertida em outras formas de energia, como a energia cinética e/ou energia potencial gravitacional.
Como podemos ver na imagem abaixo, inicialmente comprime-se a mola, mas, ao ser solta, ela adquire movimento devido à transformação da energia potencial elástica em energia cinética.
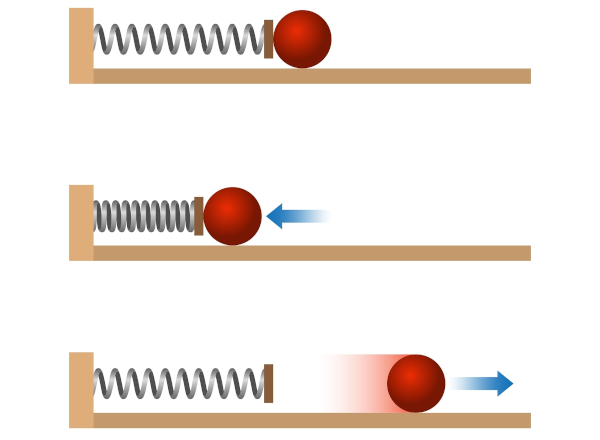
Leia também: Conservação da carga elétrica — a impossibilidade de criação ou destruição das cargas
Vantagem e desvantagem da energia potencial elástica
A energia potencial elástica tem as seguintes vantagem e desvantagem:
-
Vantagem: diminui o impacto ocasionado pelo movimento.
-
Desvantagem: faz conversão de energia de forma lenta se comparado à energia potencial gravitacional.
Diferenças entre energia potencial elástica e energia potencial gravitacional
A energia potencial elástica e a energia potencial gravitacional são formas de energia potencial relacionadas a diferentes aspectos.
-
Energia potencial elástica: associada à ação das molas e dos objetos elásticos sobre os corpos.
-
Energia potencial gravitacional: associada à variação de altura dos corpos que estão em uma região com campo gravitacional.
Exercícios resolvidos sobre energia potencial elástica
Questão 1
(Enem) Os carrinhos de brinquedo podem ser de vários tipos. Dentre eles, há os movidos a corda, em que uma mola em seu interior é comprimida quando a criança puxa o carrinho para trás. Ao ser solto, o carrinho entra em movimento enquanto a mola volta à sua forma inicial. O processo de conversão de energia que ocorre no carrinho descrito também é verificado em:
A) um dínamo.
B) um freio de automóvel.
C) um motor a combustão.
D) uma usina hidroelétrica.
E) uma atiradeira (estilingue).
Resolução:
Alternativa E
No estilingue a energia potencial elástica proveniente da mola se converte em energia cinética, provocando o lançamento do objeto.
Questão 2
(Fatec) Um bloco de massa 0,60 kg é abandonado, a partir do repouso, no ponto A de uma pista no plano vertical. O ponto A está a 2,0 m de altura da base da pista, onde está fixa uma mola de constante elástica 150 N/m. São desprezíveis os efeitos do atrito e adota-se \(g=10m/s^2\). A máxima compressão da mola vale, em metros:
A) 0,80
B) 0,40
C) 0,20
D) 0,10
E) 0,05
Resolução:
Alternativa B
Usaremos o teorema da conservação de energia mecânica para encontrarmos o valor da compressão máxima sofrida pela mola:
\(E_{m\ antes}=E_{m\ depois}\)
A energia mecânica é a soma entre as energias cinética e potencial, portanto:
\(E_{c\ antes}+E_{p\ antes}=E_{c\ depois}+E_{p\ depois}\)
Em que a energia potencial é a soma entre a energia potencial elástica e a energia potencial gravitacional. Assim temos:
\(E_{c\ antes}+E_{pel\ antes}+E_{pg\ antes}=E_{c\ depois}+E_{pel\ depois}+E_{pg\ depois}\)
Como, nesse caso, temos a energia potencial gravitacional se convertendo em energia potencial elástica, então:
![]()
\(E_{pg\ antes}=E_{pel\ depois}\)
Substituindo pelas suas respectivas fórmulas, obtemos:
\(m\cdot g\cdot h=\frac{k\cdot x^2}2\)
\(0,6\cdot 10\cdot 2=\frac{150\cdot x^2}2\)
\(12=75\cdot x^2\)
\(x^2=\frac{12}{75}\)
\(x^2=0,16\)
\(x=\sqrt{0,16}\)
\(x=0,4\ m\)
Por Pâmella Raphaella Melo
Professora de Física

