A força elástica é a força de reação dos materiais elásticos, que é contrária à força externa que a comprime ou que a estica. A fórmula da força elástica é enunciada pela lei de Hooke, que relaciona a força com a deformação da mola. Assim, podemos encontrar seu valor por meio do produto da deformação sofrida pela constante elástica do material.
Saiba mais: Força peso — a força gravitacional produzida por um segundo corpo de grande massa
Tópicos deste artigo
- 1 - Resumo sobre força elástica
- 2 - O que é força elástica?
- 3 - Qual a fórmula da força elástica?
- 4 - Trabalho da força elástica
- 5 - Como calcular a força elástica?
- 6 - Exercícios resolvidos sobre força elástica
Resumo sobre força elástica
-
A força elástica determina a deformação sofrida pela mola.
-
Seu cálculo é feito por meio da lei de Hooke.
-
A lei de Hooke determina que a força é proporcional à deformação da mola.
-
A lei de Hooke apareceu primeiramente na forma do anagrama “ceiiinosssttuv”, que representa “ut tensio, sic vis” e significa: “Como a deformação, assim a força.”
-
A constante elástica trata da facilidade ou dificuldade em deformarmos a mola e é definida pelas dimensões e natureza do material elástico.
-
O trabalho da força elástica é determinado pelo produto entre a constante elástica e o quadrado da deformação da mola, tudo dividido por dois.
-
Tanto a fórmula da força elástica quanto a do seu trabalho possuem um sinal negativo, que representa a tendência de a força ser oposta ao movimento da mola.
O que é força elástica?
A força elástica é a força associada à deformação da mola ou outros materiais, como borrachas e elásticos. Ela age no sentido contrário à força recebida pelo corpo. Ou seja, se empurrarmos a mola visando sua compressão, ela fará a mesma força, mas no sentido contrário, visando sua descompressão.
Seu cálculo é feito por meio da lei de Hooke, enunciada em 1678 por Robert Hooke (1635–1703) na forma do anagrama “ceiiinosssttuv”, a fim de reservar para si suas informações. Somente após dois anos ele o decifrou como “ut tensio, sic vis”, cujo significado é “como a deformação, assim a força”, representando a relação de proporcionalidade existente entre a força e a deformação.
→ Videoaula sobre lei de Hooke
Qual a fórmula da força elástica?
A fórmula da força elástica, ou seja, a lei de Hooke, é expressa por:
\(F_{el}=-\ k\bullet∆x\)
Em que:
\(∆x=xf-xi\)
-
\(F_{el}\): a força elástica, ou seja, a força exercida pela mola, medida em Newtons \(\).
-
k: a constante da mola, medida em [\(N/m\)].
-
\(∆x\): a variação da deformação da mola (também chamada de elongação), medida em metros [\(m\)].
-
\(x_i\): o comprimento inicial da mola, medido em metros [\(m\)].
-
\(x_f\): o comprimento final da mola, medido em metros [\(m\)].
Importante: O sinal negativo na fórmula existe em razão de a força tender a se opor ao deslocamento do corpo, visando o equilíbrio do sistema, como na figura 2 abaixo.
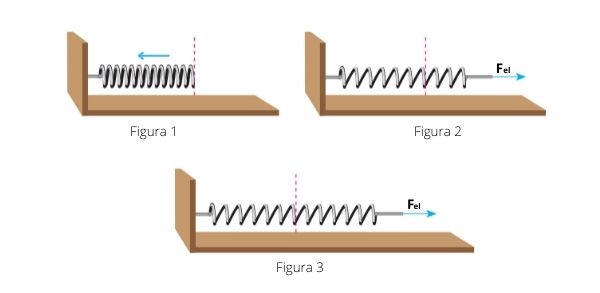
Entretanto, se \(F_{el}>0\) para \(x<0\), como na figura 1, há compressão da mola. Já se \( F_{el}<0\) para \(x>0\), como na figura 3, há distensão da mola.
→ Constante elástica
A constante elástica determina a rigidez da mola, ou seja, o quanto de força é preciso fazer para que a mola se deforme. Seu valor depende exclusivamente da natureza do material em que foi fabricada e suas dimensões. Sendo assim, quanto maior for a constante elástica, mais difícil é sua deformação.

Trabalho da força elástica
Toda força realiza trabalho. Assim, o trabalho da força elástica é encontrado por meio da fórmula:
\(W_{el}=-\left(\frac{{k\bullet x_f}^2}{2}-\frac{{k\bullet x_i}^2}{2}\right)\)
Supondo que xi=0 e chamando xf de x, temos a sua forma mais conhecida:
\(W_{el}=-\frac{{k\bullet x}^2}{2}\)
-
\(W_{el}\): o trabalho da força elástica, medido em Joules [J].
-
k: a constante da mola, medida em [N/m].
-
\(x_i\): o comprimento inicial da mola, medido em metros [m].
-
\(x_f\) ou x: o comprimento final da mola, medido em metros [m].
Leia também: Força de tração — a força aplicada sobre cordas ou fios
Como calcular a força elástica?
Do ponto de vista matemático, a força elástica é calculada por meio de sua fórmula e sempre que estivermos trabalhando com molas. Abaixo, veremos um exemplo de como calcular a força elástica.
-
Exemplo:
Sabendo que a constante elástica de uma mola é igual a 350 N/m, determine qual é a força necessária para que essa mola sofra uma deformação de 2,0 cm.
Resolução:
-
Calcularemos a força necessária para a deformação da mola por meio da lei de Hooke:
\(F_{el}=k\bullet x\)
-
Transformando a deformação de 2 cm em metros e substituindo o valor da constante da mola:
\(F_{el}=350\bullet0,02\)
\(F_{el}=7\ N\)
Exercícios resolvidos sobre força elástica
Questão 1
Quando comprimida por uma força de 10 N, uma mola tem o seu comprimento alterado em 5 cm (0,05 m). A constante elástica dessa mola, em N/m, vale cerca de:
A) 6,4 N/m
B) 500 N/m
C) 250 N/m
D) 200 N/m
E) 12,8 N/m
Resolução:
Alternativa D
Faremos o cálculo utilizando a lei de Hooke:
\(F_{el}=k\bullet x\)
\(10=k\bullet0,05\)
\(k=\frac{10}{0,05}\)
\(k=200\ N/m\)
Questão 2
Uma mola de constante elástica de 500 N/m é pressionada por uma força de 50 N. Com base nessas informações, calcule qual é, em centímetros, a deformação sofrida pela mola em razão da aplicação dessa força.
A) 100
B) 15
C) 0,1
D) 1000
E) 10
Resolução:
Alternativa E
Calcularemos a deformação da mola por meio da lei de Hooke:
\(F_{el}=k\bullet x\)
\(50=500\bullet x\)
\(x=\frac{50}{500}\)
\(x=0,1\ m\)
\(x=10\ cm\)
Por Pâmella Raphaella Melo
Professora de Física

