Sistema de numeração decimal

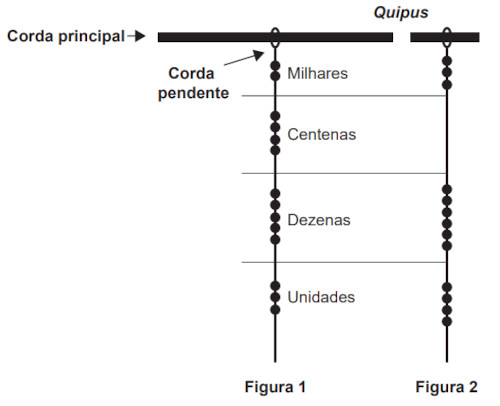
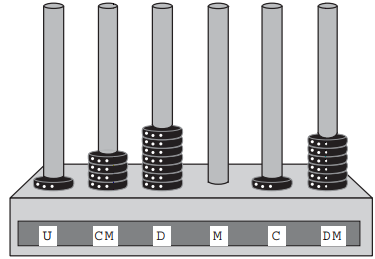
O nosso sistema de numeração, que é conhecido como sistema de numeração decimal, é baseado na quantidade de dedos que possuímos nas mãos. Nesse sistema, utilizamos as potências de dez para escrever qualquer número. Antes de realizar qualquer tipo de operação matemática ou mesmo comunicar alguma quantidade numérica, é necessário compreender a maneira como vamos nos referir a esse número. Veja a partir de agora como representar uma quantidade numérica utilizando nosso sistema de numeração.

Leia também: Notação científica – aprenda a operar números grandes de forma mais simples

Tópicos deste artigo

• 1 - Como se organiza o sistema de numeração decimal?
• 2 - Exemplos
• 3 - Ordem e classe no sistema decimal
• 4 - Exercícios resolvidos

Como se organiza o sistema de numeração decimal?

O sistema de numeração decimal é organizado a partir da junção de algarismos indo-arábicos. Com eles, é possível escrever qualquer número para representar qualquer quantidade numérica. São eles:

Cada um desse algarismos representa determinada quantidade. Essas quantidades são denominadas de unidades.

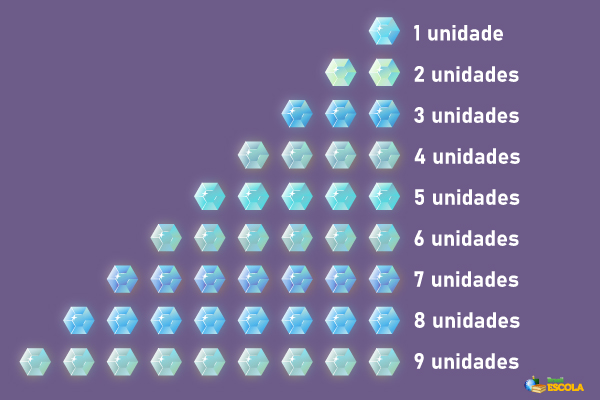
Uma das principais características desse sistema é que, a cada 10 unidades, formamos 1 dezena (10 unidades); a cada 10 dezenas, formamos 1 centena (100 unidades); a cada 10 centenas, formamos 1 unidade de milhar (1.000 unidades). Sempre que o algarismo 0 é acrescentado, devemos multiplicar a ordem por 10.

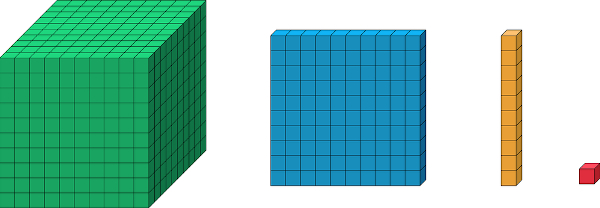
Exemplos

1. Determine quantas unidades, dezenas, centenas, unidades de milhar possui cada um dos números a seguir.

a) 504

Realizando a decomposição do número, temos:

504 → 500 + 0 + 4

• 5 centenas (5 x 100) – Quinhentas unidades
• 0 dezena (0 x 10) – Zero unidade
• 4 unidades

b) 2.471

2.471 → 2000 + 400 + 70 + 1

• 2 unidades de milhar (2 x 1000) – Duas mil unidades
• 4 centenas (4 x 100) – Quatrocentas unidades
• 7 dezenas (7 x 10) – Setenta unidades
• 1 unidade

Veja também: Números naturais – veja quais são e suas características

Ordem e classe no sistema decimal

Dado um número, cada um de seus algarismos representa uma ordem. Sempre devemos começar a análise da direita para esquerda.

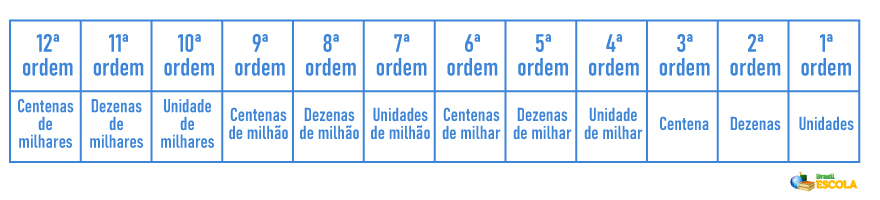
Para determinar a classe de um número, devemos separá-lo de três em três algarismos. De modo geral, fica assim:

• Classe das unidades: 1ª ordem até a 3ª ordem;
• Classe dos milhares: da 4ª ordem até a 6ª ordem;
• Classe do milhão: da 7ª ordem até a 9ª ordem;
• Classe dos milhares: 10ª ordem até a 12ª ordem e assim por diante.

Compreender a ordem e a classe de um número nos auxilia a enxergar melhor a quantidade numérica que está sendo trabalhada.

Exemplo:

a) 12345

Vamos separar o número 12345 a cada três ordens, assim:

12. 345

Veja que o 345 pertence à classe das unidades simples, portanto essa parte será lida assim: trezentos e quarenta e cinco. Já o número 12 pertence à classe das unidades de milhar e, assim, será lido como doze mil. O número 12345 é lido como: doze mil trezentos e quarenta e cinco.

Exercícios resolvidos

Questão 1 – Escreva o número por extenso e decomponha-o determinando sua ordem e classe.

a) A distância entre a Lua e a Terra, de aproximadamente 384400 quilômetros.

Resolução:

Vamos inicialmente separar as ordens desse número de três em três algarismos.

384.400

O número 400 pertence à classe das unidades simples, o número 384 pertence à classe das centenas de milhar. Portanto, esse número é lido assim:

Trezentos e oitenta e quatro mil e quatrocentos

Decompondo esse número, temos:

300.000 + 80.000 + 4.000 + 400 + 0 + 0

• 0 unidade
• 0 dezena
• 4 centenas
• 4 unidades de milhar
• 8 dezenas de milhar
• 3 centenas de milhar

b) A população no Brasil, no ano de 2017, era de 209003000 pessoas.

Resolução:

Separando de três em três algarismos, temos:

209.003.000

Os algarismos 000 pertencem à classe das unidades simples, os algarismos 003 pertencem à classe das unidades de milhar e os algarismos de 209 pertencem à classe das centenas de milhão. Assim, vamos ler o número da seguinte maneira:

Duzentos e nove milhões e três mil

Decompondo o número, temos:

209.000.000 + 3.000

• 3 unidades de milhar
• 209 centenas de milhar

c) O raio da Terra é de 6371 quilômetros.

Resolução:

De maneira análoga ao que foi feito anteriormente, vamos separar de três em três algarismos.

6.371

Observe que 371 pertence à classe das centenas simples e 6 pertence à classe da unidade de milhar. Assim, vamos ler esse número assim:

Seis mil trezentos e setenta e um

Agora vamos decompor o número:

6.000 + 300 + 70 + 1

• 1 unidade
• 7 dezenas
• 3 centenas
• 6 unidades de milhar

d) O raio do Sol, de 696340 quilômetros.

Separando os algarismos de três em três, temos:

696.340

O número 340 pertence à classe das centenas simples, enquanto 696 pertence à classe das centenas de milhar. Esse número é lido assim:

Seiscentos e noventa e seis mil trezentos e quarenta

600.000 + 90.000 + 6.000 + 300 + 40 + 0

• 0 unidade
• 4 dezenas
• 3 centenas
• 6 unidades de milhar
• 9 dezenas de milhar
• 6 centenas de milhar

Por Robson Luiz
Professor de Matemática