PUBLICIDADE
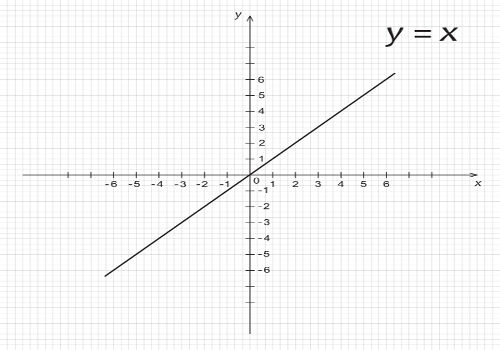
Definimos função como a relação entre duas grandezas representadas por x e y. No caso de uma função do 1º grau, sua lei de formação possui a seguinte característica: y = ax + b ou f(x) = ax + b, em que os coeficientes a e b pertencem aos números reais e diferem de zero. Esse modelo de função possui como representação gráfica a figura de uma reta, portanto, as relações entre os valores do domínio e da imagem crescem ou decrescem de acordo com o valor do coeficiente a. Se o coeficiente possui sinal positivo, a função é crescente, e caso ele tenha sinal negativo, a função é decrescente.
Função crescente: a > 0
.jpg)
Na função crescente, à medida que os valores de x aumentam, os valores de y também aumentam; ou, à medida que os valores de x diminuem, os valores de y diminuem. Observe a tabela de pontos e o gráfico da função y = 2x – 1.
|
x Não pare agora... Tem mais depois da publicidade ;) |
y |
|
-2 |
-5 |
|
-1 |
-3 |
|
0 |
-1 |
|
1 |
1 |
|
2 |
3 |
.jpg)
Função decrescente: a < 0
.jpg)
No caso da função decrescente, à medida que os valores de x aumentam, os valores de y diminuem; ou, à medida que os valores de x diminuem, os valores de y aumentam. Veja a tabela e o gráfico da função y = – 2x – 1.
|
x |
y |
|
-2 |
3 |
|
-1 |
1 |
|
0 |
-1 |
|
1 |
-3 |
|
2 |
-5 |
.jpg)
De acordo as análises feitas sobre as funções crescentes e decrescentes do 1º grau, podemos relacionar seus gráficos aos sinais. Veja:
Sinais da função do 1º grau crescente:
.jpg)
Sinais da função do 1º grau decrescente:
.jpg)
Exemplo:
Determine os sinais da função y = 3x + 9.
Fazendo y = 0, calcule a raiz da função:
3x + 9 = 0
3x = –9
x = –9/3
x = – 3
A função possui o coeficiente a = 3, no caso, é maior que zero, portanto, a função é crescente.
.jpg)
Por Marcos Noé
Graduado em Matemática