Teorema de Binet

O teorema de Binet é utilizado para facilitar os cálculos de problemas que envolvem determinantes de matrizes. Ele mostra uma relação entre os determinantes da matriz produto de duas matrizes, o que pode facilitar o cálculo. Sabemos que a multiplicação de matrizes nem sempre é um processo rápido, então, o teorema de Binet prova que o determinante da matriz produto é igual ao produto dos determinantes das matrizes, ou seja, det(A · B) = det(A) · det(B).

Leia também: O que é matriz transposta?

Tópicos deste artigo

• 1 - Resumo sobre teorema de Binet
• 2 - O que é o teorema de Binet?
• 3 - Teorema de Binet
• 4 - Como usar o teorema de Binet?
• 5 - Exercícios resolvidos sobre teorema de Binet

Resumo sobre teorema de Binet

• O teorema de Binet facilita o cálculo de determinantes de uma matriz produto.

• Segundo o teorema de Binet, det(A · B) = det(A) · det(B).

O que é o teorema de Binet?

O teorema de Binet é usado para facilitar o cálculo de determinante de um produto matricial. Acontece que calcular a multiplicação entre duas matrizes nem sempre é uma tarefa fácil, então, o teorema de Binet mostra um caminho menos árduo para se obter esse determinante. Utilizando esse teorema, em vez de calcular o produto matricial, calculamos o determinante de cada uma das matrizes, e depois multiplicamos a resposta.

Teorema de Binet

O teorema de Binet diz que:

Dadas A e B duas matrizes quadradas de mesma ordem, então, temos que:

Observação: conhecemos como matriz quadrada a matriz que possui o mesmo número de linhas e colunas, e o cálculo do determinante só é feito em matrizes quadradas, portanto, é importante que as duas matrizes sejam quadradas de mesma ordem.

Exemplo:

Conhecendo as matrizes A e B, a seguir, mostre que det(A) · det(B) = det(A · B).

Calculando separadamente, temos que:

det(A) = 1 · 4 – 2 · 3 = 4 – 6 = -2

det(B) = 1 · 1 – 3 · 2 = 1 – 6 = -5

Então, o produto det(A) · det(B) = (-2) · (-5) = 10.

Agora, vamos encontrar o produto matricial C = A · B.

Realizando a multiplicação entre as matrizes, temos que:

C₁₁ = 1 · 1 + 2 · 2 = 1 + 4 = 5

C₁₂ = 1 · 3 + 2 · 1 = 3 + 2 = 5

C₂₁ = 3 · 1 + 4 · 2 = 3 + 8 = 11

C₂₂ = 3 · 3 + 4 · 1 = 9 + 4 = 13

Então, a matriz C é a matriz a seguir:

Calculando seu determinante, temos que:

det(C) = det(A · B) = 5 · 13 – 11 · 5 = 65 – 55 = 10

Então, podemos concluir que, de fato, det(A) · det(B) = det(A · B).

Veja também: O que é uma matriz triangular?

Como usar o teorema de Binet?

Para evitar a multiplicação entre as matrizes, utilizamos o teorema de Binet, calculando o determinante das matrizes separadamente, e depois multiplicando esses determinantes, processo esse que facilita o cálculo do determinante da matriz produto.

Exemplo:

Conhecendo as matrizes A e B a seguir, então, calcule det(A · B):

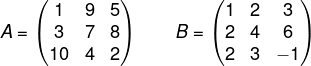
Para encontrar o valor do determinante da matriz produto, det(A · B), aplicaremos o teorema de Binet, que diz que det(A · B) = det(A) · det(B).

Como a intenção é não realizar a multiplicação das matrizes A · B, o teorema de Binet nos mostra que encontrar o determinante da matriz A · B é o mesmo que calcular o produto entre os determinantes da matriz A e da matriz B.

Para calcular os determinantes de matrizes de ordem três, no caso, det(A) e det(B), existem vários métodos, e o mais comum é a regra de Sarrus, utilizada para calcular det(A), a seguir:

Agora, calcule det(B):

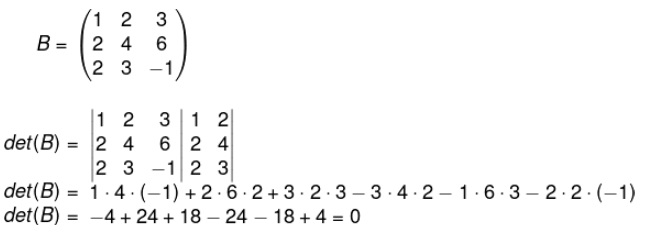
Então, aplicando o teorema de Binet, temos que:

det(A · B) = det(A) · det(B)

det(A · B) = 358 · 0

det(A · B) = 0

Exercícios resolvidos sobre teorema de Binet

Questão 1 - Um teorema muito importante é o teorema de Binet, utilizado para resolver problemas envolvendo matrizes. Por meio dele, é possível deduzir uma propriedade importante envolvendo matrizes. Segundo o teorema de Binet, podemos afirmar que:

A) det(k · A) = kⁿ · detA

B) det(A + B) = det(A) + det(B)

C) det(A · B) = det(A) · det(B)

D) k · det(A) = det(k · A)

Resolução

Alternativa C

O teorema de Binet é utilizado para calcular o determinante de uma matriz produto. Ele demonstra que det(A · B) = det(A) · det(B).

Questão 2 - Analisando as matrizes A e B a seguir, sabendo que x é um número inteiro e que det(A · B) = -35, então, o valor de x é:

A) -2

B) -1

C) 0

D) 1

E) 2

Resolução

Alternativa A

Sabemos que det(A · B) = -35, então, pelo teorema de Binet, temos que:

det(A) · det(B) = -35

Calculando cada um dos determinantes, temos que:

det(A) = -3x – 1

det(B) = 10x – 15

Então, temos que:

(-3x – 1) (10x – 15) = -35

-30x² + 45x – 10x + 15 = -35

-30x² + 35x + 15 + 35 = 0

-30x² + 35x + 50 = 0

(-30x² + 35x – 10) : 5 = 0 : 5

-6x² + 7x + 10 = 0

Encontramos uma equação do 2º grau. Aplicando a fórmula de Bhaskara, temos que:

a = -6

b = 7

c = 10

Δ = b² – 4ac

Δ = 7² – 4 · (-6) · (10)

Δ = 49 + 240

Δ = 289

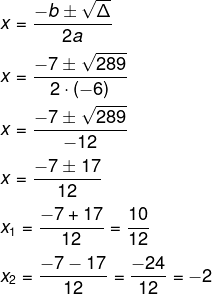
Como x é um número inteiro, então, x = -2.

 

Por Raul Rodrigues de Oliveira
Professor de Matemática