Tração

Tração, ou tensão, é nome que se dá à força que é exercida sobre um corpo por meio de cordas, cabos ou fios, por exemplo. A força de tração é particularmente útil quando se deseja que uma força seja transferida para outros corpos distantes ou ainda para alterar a direção de aplicação de uma força.

Veja também: Saiba o que estudar de Mecânica para a prova do Enem

Tópicos deste artigo

• 1 - Como calcular a força de tração?
• 2 - Tração aplicada sobre um corpo
• 3 - Tração aplicada sobre um corpo apoiado em uma superfície com atrito
• 4 - Tração entre corpos do mesmo sistema
• 5 - Tração entre bloco suspenso e bloco apoiado
• 6 - Tração no plano inclinado
• 7 - Tração entre corpo suspenso por cabo e um corpo em um plano inclinado
• 8 - Tração no pêndulo
• 9 - Exercícios resolvidos sobre tração

Como calcular a força de tração?

Para calcularmos a força de tração, devemos aplicar os nossos conhecimentos sobre as três leis de Newton, portanto, surgimos que você revise os fundamentos da Dinâmica acessando o nosso artigo sobre as Leis de Newton (basta acessar o link) antes de prosseguir com o estudo neste texto.

O cálculo da tração leva em conta como ela é aplicada, e isso depende de múltiplos fatores, como quantidade de corpos que compõem o sistema a ser estudado, o ângulo que é formado entre a força de tração e a direção horizontal e também o estado de movimento dos corpos.

A corda presa nos carros acima é usada para transferir uma força, que puxa um dos carros.

Para que possamos explicar como se calcula a tração, vamos fazê-lo com base em situações distintas, frequentemente cobradas nas provas de Física de vestibulares e no Enem.

Tração aplicada sobre um corpo

O primeiro caso é o mais simples de todos: é quando algum corpo, como o bloco representado na figura a seguir, é puxado por uma corda. Para ilustrar essa situação, escolhemos um corpo de massa m que repousa sobre uma superfície sem atrito. No caso a seguir, bem como nos demais casos, a força normal e a força peso dos corpos foram omitidas propositalmente, com o intuito de facilitar a visualização de cada caso. Observe:

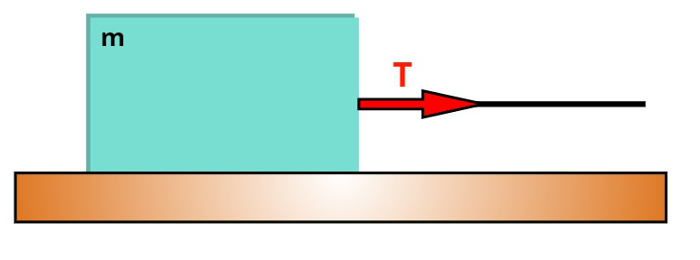
Quando a única força aplicada sobre um corpo é uma tração externa, como mostra a figura acima, essa tração será igual à força resultante sobre o corpo. De acordo com a 2ª Lei de Newton, essa força resultante será igual ao produto de sua massa pela aceleração, desse modo, a tração pode ser calculada como:

T – Tração (N)

m – massa (kg)

a – aceleração (m/s²)

Tração aplicada sobre um corpo apoiado em uma superfície com atrito

Quando aplicamos uma força de tração sobre um corpo que se encontra apoiado sobre uma superfície rugosa, essa superfície produz uma força de atrito contrária ao sentido da força de tração. De acordo com o comportamento da força de atrito, enquanto a tração mantém-se menor que a máxima força de atrito estático, o corpo continua em equilíbrio (a = 0). Agora, quando a tração exercida ultrapassa essa marca, a força de atrito se tornará uma força de atrito dinâmico.

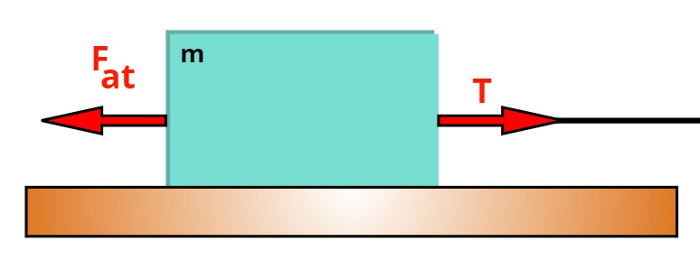
F_at – Força de atrito

No caso acima, a força de tração pode ser calculada por meio da força resultante sobre o bloco. Observe:

Tração entre corpos do mesmo sistema

Quando dois ou mais corpos de um sistema são ligados por cabos, eles se movem juntos, com a mesma aceleração. Para determinarmos a força de tração que um corpo exerce sobre o outro, fazemos o cálculo da força resultante em cada um dos corpos.

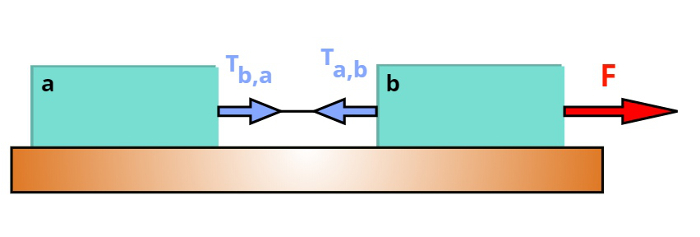
T_a,b – Tração que o corpo A faz sobre o corpo B.

T_b,a – Tração que o corpo B faz sobre o corpo A.

No caso acima, é possível ver que apenas um cabo conecta os corpos A e B, além disso, vemos que o corpo B puxa o corpo A por meio da tração T_b,a. De acordo com a terceira lei de Newton, a lei da ação e reação, a força que o corpo A exerce sobre o corpo B é igual à força que o corpo B exerce sobre o corpo A, no entanto, essas forças têm sentidos opostos.

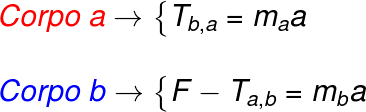
Tração entre bloco suspenso e bloco apoiado

No caso em que um corpo suspenso puxa outro corpo por meio de um cabo que passa por uma polia, podemos calcular a tração no fio ou a tração que atua em cada um dos blocos por meio da segunda lei de Newton. Nesse caso, quando não há atrito entre o bloco apoiado e a superfície, a força resultante sobre o sistema de corpos é o peso do corpo suspenso (P_B). Observe a figura a seguir, que mostra um exemplo desse tipo de sistema:

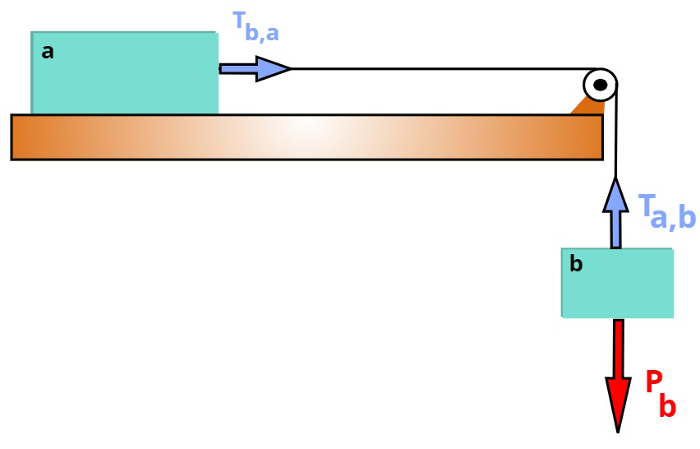
No caso acima, devemos calcular a força resultante em cada um dos blocos. Fazendo isso, encontramos o seguinte resultado:

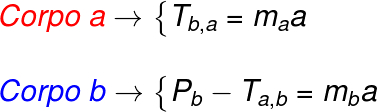
Veja também: Aprenda a resolver exercícios sobre as leis de Newton

Tração no plano inclinado

Quando um corpo que é colocado sobre um plano inclinado liso e sem atrito for tracionado por um cabo ou corda, a força de tração sobre esse corpo poderá ser calculada de acordo com a componente horizontal (P_X) do peso do corpo. Observe esse caso na figura a seguir:

P_AX – componente horizontal do peso do bloco A

P_AY – componente vertical do peso do bloco A

A tração aplicada sobre o bloco A pode ser calculada por meio da seguinte expressão:

Tração entre corpo suspenso por cabo e um corpo em um plano inclinado

Em alguns exercícios, é comum que se faça uso de um sistema em que o corpo que se encontra apoiado sobre o plano inclinado é tracionado por um corpo suspenso, por meio de uma corda que passa por uma roldana.

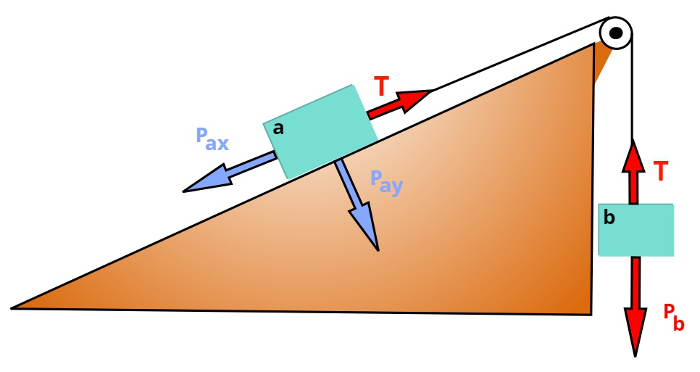
Na figura acima, desenhamos as duas componentes da força peso do bloco A, P_AX e P_AY. A força responsável por mover esse sistema de corpos é a resultante entre o peso do bloco B, suspenso, e a componente horizontal do peso do bloco A:

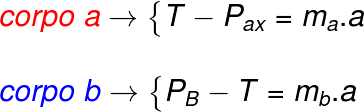
Tração no pêndulo

No caso do movimento de pêndulos, que se movem de acordo com uma trajetória circular, a força de tração produzida pelo fio atua como uma das componentes da força centrípeta. No ponto mais baixo da trajetória, por exemplo, a força resultante é dada pela diferença entre a tração e o peso. Observe um esquema desse tipo de sistema:

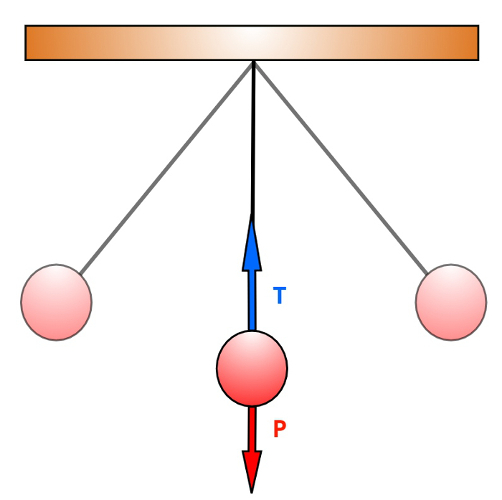
No ponto mais baixo do movimento pendular, a diferença entre tração e peso produz a força centrípeta.

Como dito, a força centrípeta é a força resultante entre a força de tração e a força peso, desse modo, teremos o seguinte sistema:

F_CP – força centrípeta (N)

Com base nos exemplos mostrados acima, é possível ter uma ideia geral de como se deve resolver exercícios que exijam o cálculo da força de tração. Assim como qualquer outro tipo de força, a força de tração deve ser calculada mediante a aplicação dos nossos conhecimentos sobre as três leis de Newton. No tópico a seguir, apresentamos alguns exemplos de exercícios resolvidos sobre a força de tração para que você possa compreendê-la melhor.

Exercícios resolvidos sobre tração

Questão 1 - (IFCE) Na figura abaixo, o fio inextensível que une os corpos A e B e a polia têm massas desprezíveis. As massas dos corpos são mA = 4,0 kg e mB = 6,0 kg. Desprezando-se o atrito entre o corpo A e a superfície, a aceleração do conjunto, em m/s², é de (considere a aceleração da gravidade 10,0 m/s²)?

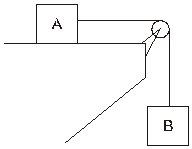
a) 4,0

b) 6,0

c) 8,0

d) 10,0

e) 12,0

Gabarito: Letra B

Resolução:

Para resolvermos o exercício, é necessário aplicar a segunda lei de Newton ao sistema como um todo. Fazendo isso, vemos que a força peso é a resultante que faz todo o sistema mover-se, desse modo, devemos resolver o seguinte cálculo:

Questão 2 - (UFRGS) Dois blocos, de massas m₁=3,0 kg e m₂=1,0 kg, ligados por um fio inextensível, podem deslizar sem atrito sobre um plano horizontal. Esses blocos são puxados por uma força horizontal F de módulo F = 6 N, conforme a figura a seguir (desconsidere a massa do fio).

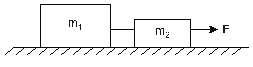
A tensão no fio que liga os dois blocos é

a) zero

b) 2,0 N

c) 3,0 N

d) 4,5 N

e) 6,0 N

Gabarito: Letra D

Resolução:

Para resolver o exercício, basta perceber que a única força que move o bloco de massa m₁ é a força de tração que o fio faz sobre ele, portanto, ela é a força resultante. Portanto, para resolvermos esse exercício, encontramos a aceleração do sistema e, em seguida, fazemos o cálculo da tração:

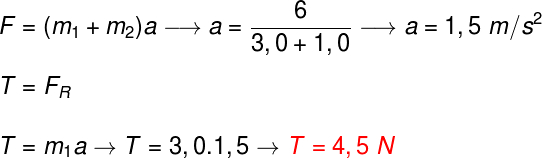
Questão 3 - (EsPCEx) Um elevador possui massa de 1500 kg. Considerando a aceleração da gravidade igual a 10 m/s², a tração no cabo do elevador, quando ele sobe vazio, com uma aceleração de 3m/s², é de:

a) 4500 N

b) 6000 N

c) 15500 N

d) 17000 N

e) 19500 N

Gabarito: Letra E

Resolução:

Para calcularmos a intensidade da força de tração exercida pelo cabo sobre o elevador, aplicamos a segunda lei de Newton, desse modo, descobrimos que a diferença entre a tração e o peso é equivalente à força resultante, daí concluímos que:

Questão 4 - (CTFMG) A figura a seguir ilustra uma máquina de Atwood.

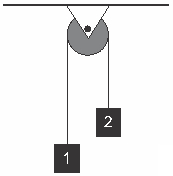
Supondo-se que essa máquina possua uma polia e um cabo de massas insignificantes e que os atritos também são desprezíveis, o módulo da aceleração dos blocos de massas iguais a m₁ = 1,0 kg e m₂ = 3,0 kg, em m/s², é:

a) 20

b) 10

c) 5

d) 2

Gabarito: Letra C

Resolução:

Para calcularmos a aceleração desse sistema, é necessário notar que a força resultante é determinada pela diferença entre os pesos dos corpos 1 e 2, fazendo isso, basta aplicar a segunda lei de Newton:

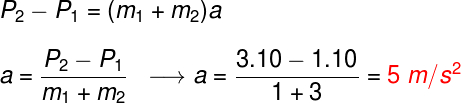
Por Me. Rafael Helerbrock