A alavanca é uma máquina simples constituída de ponto de apoio, força resistente e força potente com a função de executar tarefas que seriam árduas sem o seu uso. Ela facilita a realização de uma atividade por aumentar a força de aplicação sobre um corpo quando sustentado em um ponto fixo. Os seus tipos são alavanca interfixa, alavanca inter-resistente e alavanca interpotente.
Leia também: Roldanas ou polias — mecanismos facilitadores do transporte de corpos
Tópicos deste artigo
- 1 - Resumo sobre a alavanca
- 2 - O que é alavanca?
- 3 - Tipos de alavanca
- 4 - Funcionamento da alavanca
- 5 - Fórmula da alavanca
- 6 - Exercícios resolvidos sobre alavanca
Resumo sobre a alavanca
- A alavanca é uma máquina simples que facilita a realização de uma atividade por aumentar a força de aplicação sobre um corpo quando sustentado em um ponto fixo.
- As alavancas podem ser interfixa, inter-resistente e interpotente.
- Arquimedes foi o responsável pela explicação do princípio de funcionamento das alavancas.
- As alavancas funcionam pela relação da força potente e força resistente com as suas distâncias até o ponto de apoio.
- Quanto mais longe do ponto de apoio for empregado uma força potente, menor esforço será necessário para realizar o movimento.
- A fórmual da alavanca é a seguinte:
\(F_p\cdot d_p=F_r\cdot d_r\)
O que é alavanca?
A alavanca é um objeto rígido, algumas vezes dotado de eixos fixos ou giratórios, que consegue aumentar a força de aplicação sobre um corpo quando sustentado em um ponto fixo. Em razão disso, a alavanca consegue simplificar a execução de um trabalho, como elevar e abaixar corpos massivos, recortar, quebrar, remover tampas e muitas outras atividades. A alavanca é composta de três elementos:
- Ponto de apoio: é o ponto que possibilita que a alavanca rotacione.
- Força resistente: é a força que resiste ao movimento.
- Força potente: é a força aplicada a fim de executar o movimento.
Tipos de alavanca
Os tipos de alavanca são: alavanca interfixa, alavanca inter-resistente e alavanca interpotente.
→ Alavanca interfixa
A alavanca interfixa é aquela em que o ponto de apoio se localiza entre a força potente e a força resistente, como demonstrado na imagem abaixo.
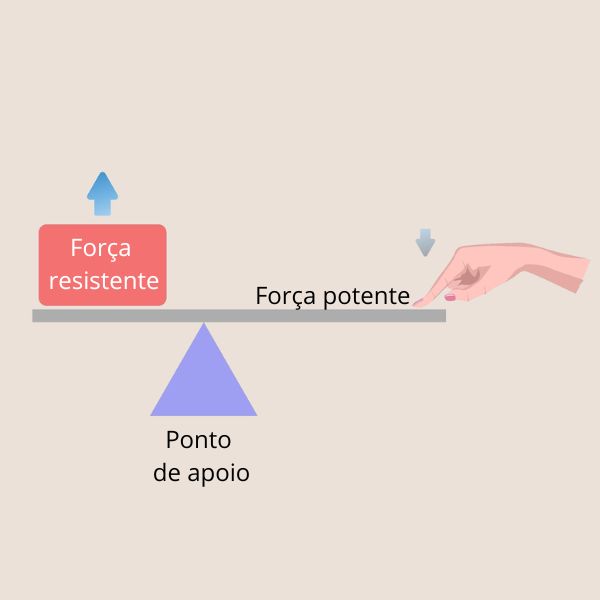
Em nosso cotidiano encontramos diversos exemplos de alavancas interfixas, como a gangorra, o alicate, a tesoura e o martelo.
→ Alavanca inter-resistente
A alavanca inter-resistente é aquela em que a força resistente se localiza entre a força potente e o ponto de apoio, como demonstrado na imagem abaixo.
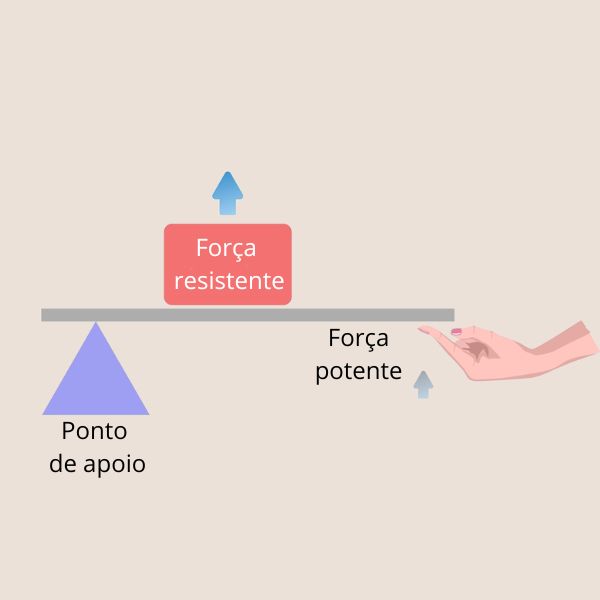
Em nosso cotidiano encontramos diversos exemplos de alavancas inter-resistentes, como o abridor de garrafas, os carrinhos de mão e o quebra-nozes.
→ Alavanca interpotente
A alavanca interpotente é aquela em que a força potente se localiza entre a força resistente e o ponto de apoio, como demonstrado na imagem abaixo.
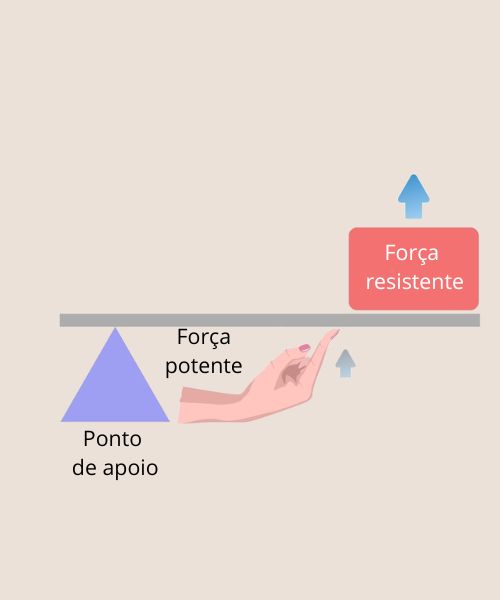
Em nosso cotidiano encontramos diversos exemplos de alavancas interpotentes, como o cortador de unhas, a pinça e em alguns exercícios de musculação.
Funcionamento da alavanca
O princípio de funcionamento da alavanca foi esclarecido no século III a.C. pelo polímata Arquimedes de Siracusa (287 a.C. – 212 a.C.). De acordo com ele, as alavancas funcionam devido à relação existente entre as posições em que aplicamos as forças potente e resistente e suas distâncias até o ponto de apoio, expressadas matematicamente pela fórmula da alavanca. Assim, quanto mais afastada for a aplicação da força potente sobre o ponto de apoio, menor será o esforço para movimentar o corpo (como pessoas, portas, objetos).
Veja também: Como funcionam os airbags?
Fórmula da alavanca
\(F_p\cdot d_p=F_r\cdot d_r\)
- Fp → força potente, medida em Newton .
- dp → distância da força potente, medida em metros .
- Fr → força resistente, medida em Newton .
- dr → distância da força resistente, medida em metros .
Exercícios resolvidos sobre alavanca
Questão 1
(Encceja) A imagem representa uma balança utilizada para a medida da massa de uma fruta. A massa colocada no prato direito da balança é de 100 g e o sistema encontra-se em equilíbrio.
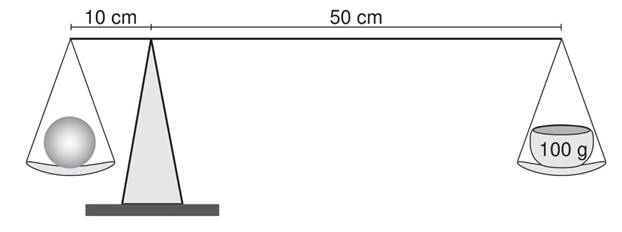
A massa dessa fruta, em grama, é
A) 100
B) 120
C) 500
D) 600
Resolução:
Alternativa C.
Calcularemos a massa da fruta através da fórmula da alavanca:
\(F_1\cdot d_1=F_2\cdot d_2\)
A força atuante na fruta e na massa é a força peso, então:
\(P_1\cdot d_1=P_2\cdot d_2\)
\(m_1\cdot g\cdot d_1=m_2\cdot g\cdot d_2\)
\(m_1\cdot10\cdot10=100\cdot10\cdot50\)
\(m_1\cdot100=50000\)
\(m_1=\frac{50000}{100}\)
\(m_1=500\ g\)
Questão 2
(Enem) Em um experimento, um professor levou para a sala de aula um saco de arroz, um pedaço de madeira triangular e uma barra de ferro cilíndrica e homogênea. Ele propôs que fizessem a medição da massa da barra utilizando esses objetos. Para isso, os alunos fizeram marcações na barra, dividindo-a em oito partes iguais, e em seguida apoiaram-na sobre a base triangular, com o saco de arroz pendurado em uma de suas extremidades, até atingir a situação de equilíbrio.

Nessa situação, qual foi a massa da barra obtida pelos alunos?
A) 3,00 kg
B) 3,75 kg
C) 5,00 kg
D) 6,00 kg
E) 15,00 kg
Resolução:
Alternativa E.
Calcularemos a massa da barra obtida pelos alunos através da fórmula da alavanca:
\(F_p\cdot d_p=F_r\cdot d_r\)
A força resistente é a força que o arroz faz, então:
\(F_p\cdot d_p=F_{arroz}\cdot d_{arroz}\)
A potente é a força peso, então:
\(P_p\cdot d_p=P_{arroz}\cdot d_{arroz}\)
\(m_p\cdot g\cdot d_p=m_{arroz}\cdot g\cdot d_{arroz}\)
\(m_p\cdot10\cdot1=5\cdot10\cdot3\)
\(m_p\cdot10\cdot1=5\cdot10\cdot3\)
\(m_p\cdot10=150\)
\(m_p=\frac{150}{10}\)
\(m_p=15\ kg\)
Fontes
NUSSENZVEIG, Herch Moysés. Curso de física básica: Mecânica (vol. 1). 5 ed. São Paulo: Editora Blucher, 2015.
HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Mecânica. 8. ed. Rio de Janeiro, RJ: LTC, 2009.

