O plano inclinado com atrito é considerado uma máquina simples, bem como é uma das aplicações mais comuns e cotidianas das leis de Newton. Trata-se de uma superfície reta, disposta segundo um ângulo oblíquo em relação à direção horizontal, na qual se dispõe um objeto que fica sujeito à ação das forças peso e atrito, essa última, produzida pela força de compressão, conhecida como força normal, atua entre a superfície e o corpo.
Para melhor compreensão do tema em questão, vamos revisar as ideias de plano inclinado e de força de atrito do plano inclinado. Após isso, a resolução de exercícios que envolvem planos inclinados com atrito possibilitará um bom entendimento sobre como devem ser aplicadas as três leis de Newton, em especial, o princípio fundamental da dinâmica.
Veja também: Como resolver exercícios sobre as leis de Newton – passo a passo
Tópicos deste artigo
- 1 - Plano inclinado
- 2 - Força de atrito no plano inclinado
- 3 - Plano inclinado com atrito
- 4 - Exercícios resolvidos sobre plano inclinado com atrito
Plano inclinado
Plano inclinado é um tipo de máquina simples que consiste em uma superfície disposta em um certo ângulo com a direção horizontal. Dessa maneira, quando um corpo é apoiado sobre essa superfície, a força peso que atua sobre o corpo na direção vertical passa a apresentar uma componente horizontal, fazendo com que o corpo possa deslizar pelo plano, caso nenhuma outra força atue sobre ele.

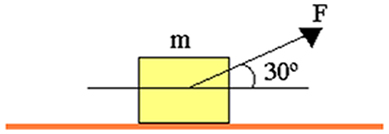
A figura seguinte mostra uma situação em que um corpo de massa m encontra-se apoiado sobre um plano inclinado de um ângulo θ em relação à direção x (horizontal). Perceba que, em razão da inclinação, a força peso (P) passa a apresentar as componentes Px e Py.
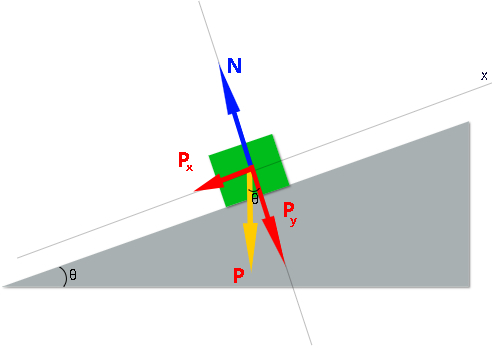
Pela análise da figura, é possível perceber que Px é o cateto oposto (C.O.) ao ângulo θ e que Py, consequentemente, é o cateto adjacente (C.A) a esse ângulo, por esse motivo, essas componentes podem ser escritas em termos das funções seno e cosseno, da seguinte maneira:
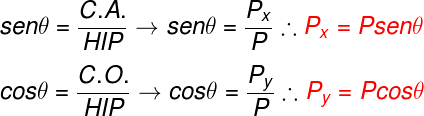
Consequentemente, ao resolver-se exercícios que envolvam um plano inclinado, é necessário que a 2ª lei de Newton seja aplicada tanto na direção x, quanto na direção y. Para tanto, dizemos que a soma vetorial das forças (força resultante), na direção x e na direção y, deve ser igual ao produto da massa pelas componentes x e y da aceleração:
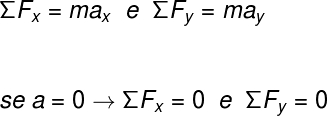
É importante lembrar que caso o corpo encontre-se em repouso ou, ainda, deslizando com velocidade constante, então sua aceleração será necessariamente igual a 0, de acordo com a 1º lei de Newton, a lei da inércia.
Força de atrito no plano inclinado
A força de atrito (Fat) surge quando há contato entre superfícies que não são perfeitamente lisas, essa força tem origem microscópica e é proporcional à força de compressão que um corpo exerce sobre o outro, conhecida como força normal.
A fórmula usada para o cálculo da força de atrito é mostrada a seguir, confira:
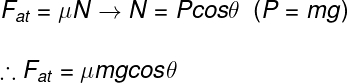
μ – coeficiente de atrito
m – massa (kg)
g – gravidade (m/s²)
Na imagem anterior, também é mostrado que a força normal N é, pelo menos em boa parte dos exercícios, igual à componente y do peso, isso será verdade sempre que não houver quaisquer outras forças, além das forças peso e normal, atuando na direção y.
Existem dois casos de força de atrito, a força de atrito estático e a força de atrito dinâmico. O primeira caso aplica-se à situação em que o corpo está em repouso, já o segundo está relacionado à situação em que o corpo desliza sobre o plano inclinado.
A força de atrito estático é sempre proporcional à força que tenta colocar o corpo em movimento, e por isso, esta aumenta na mesma proporção que aquela, até que o corpo comece a deslizar sobre o plano inclinado. Nesse caso, para calcularmos a força de atrito, devemos usar o coeficiente de atrito dinâmico, que sempre tem um valor menor que o do coeficiente de atrito estático.
Lembre-se de que a força de atrito sempre atua na direção oposta a que o corpo desliza sobre o plano inclinado, e isso afeta o sinal algébrico atribuído a ela durante a resolução de acordo com a orientação positiva das direções x e y.
Veja também: Queda livre – o que é, exemplos, fórmula e exercícios
Plano inclinado com atrito
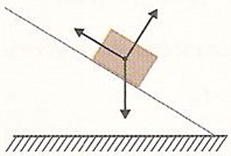
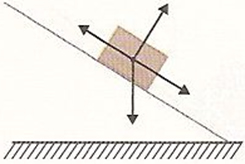
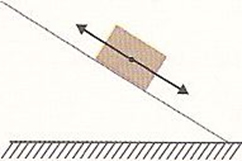
O plano inclinado com atrito, em sua forma mais simples, envolve a ação da força peso e da força de atrito. Há três situações que podem ser consideradas nesse sentido: a primeira, em que o corpo encontra-se estático; a segunda, quando o corpo desliza com velocidade constante; e a terceira, em que o corpo desliza de forma acelerada.
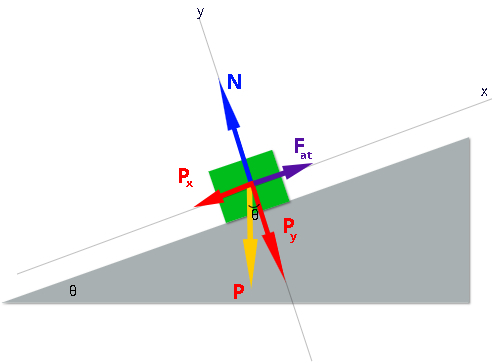
No primeiro e no segundo caso, a força resultante nas direções x e y é nula. O que os difere, de fato, é apenas o coeficiente de atrito, que, no primeiro caso, é estático, e, no segundo, é dinâmico. No último caso, utiliza-se o coeficiente de atrito dinâmico, entretanto, a força resultante é não nula e, por isso, é igual à massa do corpo multiplicada pela aceleração.
Para por-se em prática e compreender-se melhor a teoria do plano inclinado com atrito, é necessário resolver-se alguns exercícios, vamos lá?
Veja também: Os tópicos mais importantes da física mecânica para o Enem
Exercícios resolvidos sobre plano inclinado com atrito
Questão 1) (UERJ) Um bloco de madeira encontra-se em equilíbrio sobre um plano inclinado de 45º em relação ao solo. A intensidade da força que o bloco exerce perpendicularmente ao plano inclinado é igual a 2,0 N. Entre o bloco e o plano inclinado, a intensidade da força de atrito, em newtons, é igual a:
a) 0,7
b) 1,0
c) 1,4
d) 2,0
Gabarito: letra D
Resolução:
O enunciado afirma que o bloco encontra-se em equilíbrio, isso significa que a força resultante sobre ele deve ser igual a 0, além disso, a força normal entre o bloco e o plano inclinado é igual a 2,0 N. Com base nesas informações, o exercício pede-nos que calculemos a intensidade da força de atrito.
Se, nessa resolução, utilizássemos a fórmula da força de atrito indiscriminadamente, perceberíamos que alguns dados não foram informados pelo enunciado, como o coeficiente de atrito estático, além disso, estaríamos cometendo um erro, já que essa fórmula permitiria calcularmos o valor máximo da força de atrito estático e não a força de atrito estático que, necessesariamente, está sendo exercida sobre o bloco.
Portanto, para resolver o exercício, é preciso perceber que, uma vez que o bloco está parado, as forças na direção x, aquela que é paralela ao plano inclinado, anulam-se, logo, a componente do peso na direção x (Px) e a força de atrito, que é oposta a essa componente, têm módulos iguais, confira:
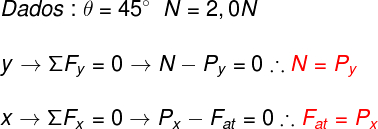
Depois de termos considerado a soma vetorial das direções x e y, partimos para a resolução das expressões obtidas na cor vermelha, observe:
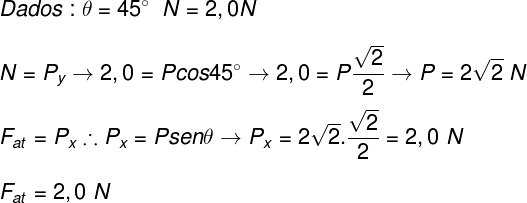
No cálculo anterior, descobrimos qual era o peso P do corpo, em seguida, com base na igualdade entre a força de atrito e Px, calculamos o valor dessa força, que é igual a 2,0 N, portanto, a alternativa correta é a letra D.
Questão 2) (PUC-RJ) Um bloco escorrega a partir do repouso por um plano inclinado que faz um ângulo de 45º com a horizontal. Sabendo que durante a queda a aceleração do bloco é de 5,0 m/s² e considerando g = 10m/s², podemos dizer que o coeficiente de atrito cinético entre o bloco e o plano é:
a) 0,1
b) 0,2
c) 0,3
d) 0,4
e) 0,5
Gabarito:
Resolução:
Para resolver o exercício, devemos aplicar a 2ª lei de Newton nas direções x e y. Vamos começar fazendo isso para a direção x, para tanto, devemos lembrar que a força resultante nessa direção deve ser igual à massa vezes a aceleração:
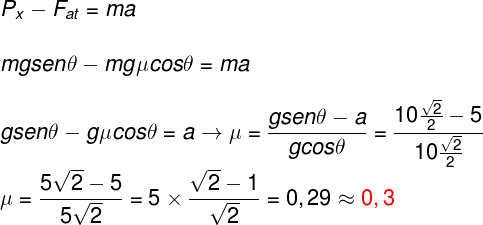
Depois de substituirmos Px e Fat, simplificamos as massas presentes em todos os termos, depois, reorganizamos esses termos, para que o coeficiente de atrito ficasse isolado, em seguida, substituimos os valores na fórmula obtida e aplicamos a propriedade distributiva no último passo, obtendo um valor igual a 0,3 para o coeficiente de atrito, logo, a alternativa correta é a letra c.
Por Rafael Helerbrock
Professor de Física