Estática

A estática é a área da Mecânica Clássica responsável por estudar os sistemas de partículas ou de corpos rígidos em estado de equilíbrio. Nessa área estudamos conceitos como o centro de massa, torque, momento angular, alavanca e equilíbrio.

Leia também: Cinemática — área da Mecânica que estuda o movimento dos corpos

Tópicos deste artigo

• 1 - Resumo sobre estática
• 2 - O que a estática estuda?
• 3 - Para que serve a estática?
• 4 - Conceitos importantes da estática
• 5 - Principais fórmulas da estática
  • → Fórmulas do centro de massa
  • → Fórmula da alavanca
  • → Fórmulas do torque
  • → Fórmula do momento angular
• 6 - Exercícios resolvidos sobre estática

Resumo sobre estática

• O estudo da estática possibilita a construção e estabilidade de edifícios, pontes, automóveis, monumentos, gangorras e muito mais.
• Na estática são estudados os conceitos e aplicações de centro de massa, equilíbrio, alavanca, torque, momento angular.
• O centro de massa é calculado através da média aritmética da massa das partículas e suas posições no sistema.
• O torque é calculado através do produto entre a força produzida, o braço de alavanca e o ângulo entre a distância e a força.
• O momento angular é calculado através do produto entre a distância do objeto ao eixo de rotação, o momento linear e o ângulo entre a distância e o momento linear.

O que a estática estuda?

A estática estuda os corpos rígidos ou partículas em repouso, estando estáticos, em razão das suas forças e momentos estarem se anulando em todas as direções, provocando o equilíbrio, com

 isso podemos determinar as forças internas que estão sobre esse sistema.

Para que serve a estática?

O estudo da estática é amplamente aplicado nas construções de pontes, edifícios, casas, móveis, automóveis, portas, janelas, enfim, tudo aquilo que necessita de equilíbrio. O estudo das alavancas permite compreender e fabricar os carrinhos de mão, martelos, quebra-nozes, pegadores de massa, varas de pesca, gangorras e muito mais. Além disso, o estudo do momento angular possibilita o aperfeiçoamento dos giros dos patinadores, rodas das bicicletas e cadeira giratória.

Veja também: Qual é o conceito de força?

Conceitos importantes da estática

• Centro de massa: é o ponto em que se acumula toda a massa de um sistema físico ou de uma partícula. Nem sempre ele está no corpo, como no caso de um anel, em que o seu
• centro de massa está no centro, onde não tem material.  Para saber mais sobre esse conceito, clique aqui.
• Equilíbrio: é a situação em que o somatório de todas as forças e momentos sobre um corpo é nulo, mantendo o corpo inalterado.
• Alavanca: é uma máquina simples capaz de simplificar a execução de uma tarefa, podendo ser interfixa, interpotente e inter-resistente.
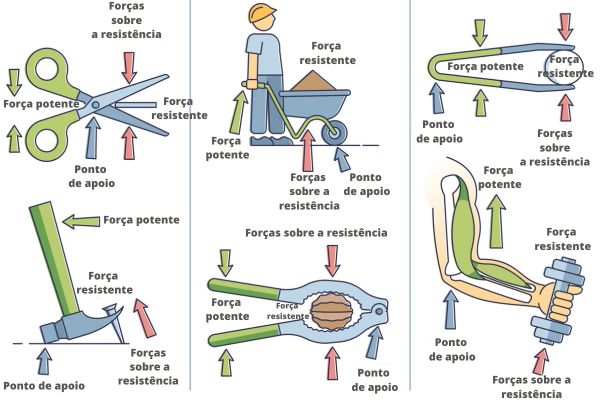
  • A alavanca interfixa possui o ponto de apoio entre a força potente e a força resistente, como é o caso da tesoura, alicate, gangorra e martelo.
  • A alavanca inter-resistente possui a força resistente entre a força potente e o ponto de apoio, como é o caso do quebra-nozes, abridor de garrafas, carrinho de mão.
  • A alavanca interpotente possui a força potente entre a força resistente e o ponto de apoio, como é o caso da pinça, cortador de unhas, alguns exercícios de musculação.

• Torque: também chamado de momento de força, é uma grandeza física que ocorre quando aplicamos uma força sobre um corpo capaz de rotacionar, girar, como abrir uma porta giratória. Saiba mais sobre esse conceito, clicando aqui.
• Momento angular: é uma grandeza física que informa a respeito da quantidade de movimento de corpos que estão rotacionando, girando ou fazendo curvas.

Principais fórmulas da estática

→ Fórmulas do centro de massa

\(X_{CM}=\frac{m_1\cdot x_1+m_2\cdot x_2 +m_3\cdot x_3}{m_1+m_2+m_3 }\)

e

\(Y_{CM}=\frac{m_1\cdot y_1+m_2\cdot y_2 +m_3\cdot y_3}{m_1+m_2+m_3 }\)

x_CM é a posição do centro de massa do sistema de partículas no eixo horizontal.

y_CM é a posição do centro de massa do sistema de partículas no eixo vertical.

m₁, m₂ e m₃ são as massas das partículas.

x₁, x₂ e x₃ são as posições das partículas no eixo horizontal.

y₁, y₂ e y₃ são as posições das partículas no eixo vertical.

→ Fórmula da alavanca

\(F_p\cdot d_p=F_r\cdot d_r\)

F_p é a força potente, medida em Newton [N].

d_p é a distância da força potente, medida em metros [m].

F_r é a força resistente, medida em Newton [N].

d_r é a distância da força resistente, medida em metros [m].

→ Fórmulas do torque

\(τ=r\cdot F\cdot sinθ\)

τ é o torque produzido, medido em N∙m.

r é a distância do eixo de rotação, também chamado de braço de alavanca, medida em metros [m].

F é a força produzida, medida em Newton [N].

θ é o ângulo entre a distância e a força, medido em graus [°].

Quando o ângulo for de 90º, a fórmula de torque pode ser representada por:

\(τ=r\cdot F\)

τ é o torque produzido, medido em [N∙m].

r é a distância do eixo de rotação, também chamado de braço de alavanca, medida em metros [m].

F é a força produzida, medida em Newton [N].

→ Fórmula do momento angular

\(L=r\cdot p\cdot sinθ\)

L é o momento angular, medido em [kg∙m^2/s].

r é a distância entre o objeto e o eixo de rotação ou raio, medida em metros [m].

p é o momento linear, medido em [kg∙m/s].

θ é o ângulo entre o r e Q, medido em graus [°].

Saiba mais: Hidrostática — ramo da Física que estuda os fluidos em condições de equilíbrio estático

Exercícios resolvidos sobre estática

01) (UFRRJ-RJ) Na figura abaixo, suponha que o menino esteja empurrando a porta com uma força F_m = 5 N, atuando a uma distância de 2 m das dobradiças (eixo de rotação), e que o homem exerça uma força F_h = 80 N, a uma distância de 10 cm do eixo de rotação.

Nessas condições, pode-se afirmar que:

a) a porta estaria girando no sentido de ser fechada.

b) a porta estaria girando no sentido de ser aberta.

c) a porta não gira em nenhum sentido.

d) o valor do momento aplicado à porta pelo homem é maior que o valor do momento aplicado pelo menino.

e) a porta estaria girando no sentido de ser fechada, pois a massa do homem é maior que a massa do menino.

Resolução:

Alternativa B. A porta estaria girando no sentido de ser aberta. Para isso, basta calcularmos o torque do homem, através da fórmula:

\(τ_h=r\cdot F\)

\(τ_h=0,1\cdot80\)

\(τ_h=8N\cdot m\)

E o torque do menino:

\(τ_m=r\cdot F\)

\(τ_m=2\cdot 5\)

\(τ_m=10N\cdot m\)

Então, é possível perceber que o torque do menino é maior que o torque do homem, por isso a porta está abrindo.

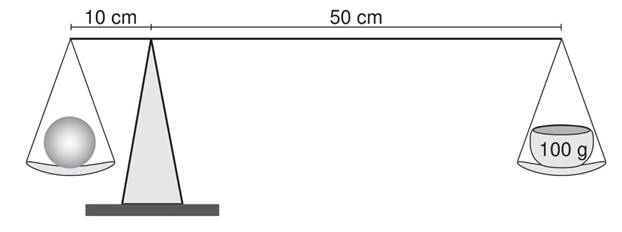
02) (Enem) Em um experimento, um professor levou para a sala de aula um saco de arroz, um pedaço de madeira triangular e uma barra de ferro cilíndrica e homogênea. Ele propôs que fizessem a medição da massa da barra utilizando esses objetos. Para isso, os alunos fizeram marcações na barra, dividindo-a em oito partes iguais, e em seguida apoiaram-na sobre a base triangular, com o saco de arroz pendurado em uma de suas extremidades, até atingir a situação de equilíbrio.

Nessa situação, qual foi a massa da barra obtida pelos alunos?

a) 3,00 kg

b) 3,75 kg

c) 5,00 kg

d) 6,00 kg

e) 15,00 kg

Resolução:

Alternativa E. Calcularemos a massa da barra obtida pelos alunos, através da fórmula da alavanca, em que comparamos a força potente com a força resistente:

\(F_p\cdot d_p=F_r\cdot d_r\)

A força que o arroz faz é a que resiste ao movimento da barra, então:

\(F_p\cdot d_p=F_{arroz}\cdot d_{arroz}\)

A força atuante sobre o arroz e sobre a força potente é a força peso, então:

\(P_p\cdot d_p=P_{arroz}\cdot d_{arroz}\)

\(m_pg\cdot d_p=m_{arroz}\cdot g\cdot d_{arroz}\)

\(m_p\cdot10\cdot1=5\cdot10\cdot3\)

\(m_p\cdot10=150\)

\(m_p=\frac{150}{10}\)

\(m_p=15 kg\)

Fontes

HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Mecânica. 8. ed. Rio de Janeiro, RJ: LTC, 2009.

NUSSENZVEIG, Herch Moysés. Curso de física básica: Mecânica (vol. 1). 5 ed. São Paulo: Blucher, 2015.