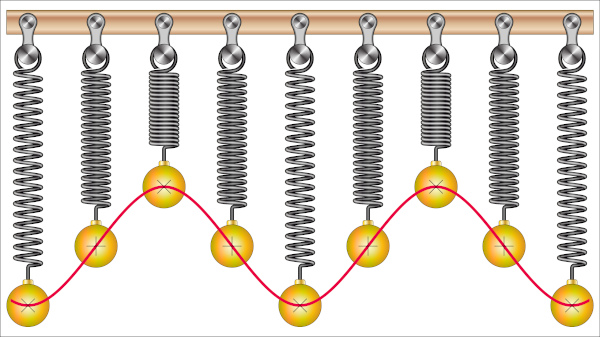
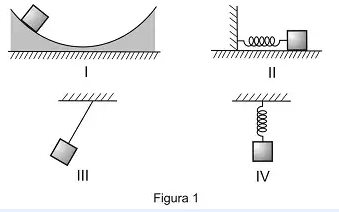
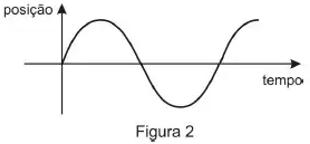
O movimento oscilatório é caracterizado por uma oscilação que acontece quando retiramos o corpo da sua posição de equilíbrio. Ele pode ser períodico, em que não há perda de energia, ou pode ser não períodico, em que há perda de energia durante o movimento.
Leia também: Como saber a quantidade de movimento?
Tópicos deste artigo
- 1 - Resumo sobre o movimento oscilatório
- 2 - O que é movimento oscilatório?
- 3 - Exemplos de movimento oscilatório
- 4 - Período do movimento oscilatório
- 5 - Fórmulas do movimento oscilatório
- 6 - Exercícios resolvidos sobre movimento oscilatório
Resumo sobre o movimento oscilatório
-
Pode ser descrito como um movimento de vai e vem dos corpos, podendo estes voltarem ou não para o ponto de início.
-
É caracterizado por ser períodico ou não e também pela inversão no sentido do movimento.
-
Suas formas mais comuns se dão pelo pêndulo simples e no movimento harmônico simples (MHS).
-
São exemplos dele o movimento do bater de asas e o do pular a corda.
-
Seu período é o inverso da frequência, sendo o intervalo de tempo necessário para finalizar uma oscilação.
-
Uma das formas de descrevê-lo é pela função horária da posição do movimento harmônico simples (MHS), que tem a seguinte fórmula:
\(x(t)=A\cdot cos(ωt+ϕ)\)
-
Outra forma de descrevê-lo é pela função horária da velocidade do movimento harmônico simples (MHS), que tem a seguinte fórmula:
\(v(t)=-ω\cdot A\cdot sin(ωt+ϕ)\)
-
Outra forma ainda de descrevê-lo é pela função horária da aceleração do movimento harmônico simples (MHS), que tem a seguinte fórmula:
\(a(t)=ω^2\cdot A\cdot cos(ωt+ϕ)\)
O que é movimento oscilatório?
Também conhecido como oscilação, o movimento oscilatório ocorre quando deslocamos um corpo (ou partícula) da sua posição de equilíbrio (posição de repouso) e o soltamos, o que faz com que ele instantaneamente busque retornar a essa posição por meio de um movimento de “vai e volta”, que corresponde a uma inversão no sentido do movimento.
Esse movimento pode ser períodico, quando a posição, velocidade e aceleração do corpo que está oscilando se repetem com o mesmo intervalo de tempo, sem perdas de energia para o meio, como é o caso do movimento de uma mola no vácuo; ou pode ser não períodico, quando o corpo oscila e vai perdendo energia até que fique em repouso, como é o caso do pêndulo de Newton.
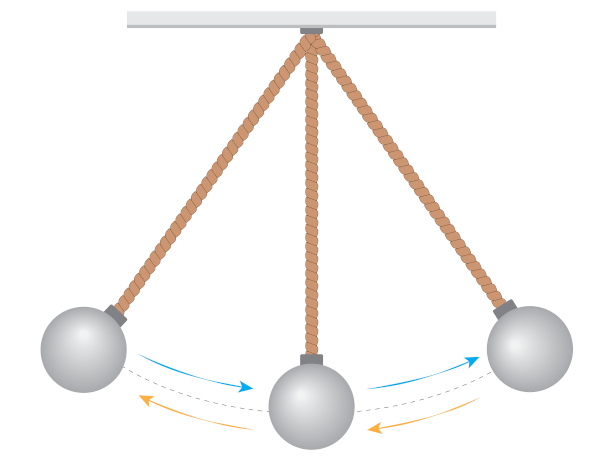
Todo movimento que oscila pode ser considerado uma forma de movimento oscilatório, como o movimento circular uniforme (movimento em trajetórias circulares), o movimento de um pêndulo simples (movimento de um corpo preso em um fio), ou o movimento harmônico simples (movimento oscilatório períodico).
Exemplos de movimento oscilatório
Existem diversos exemplos do movimento oscilatório que podem ser observados em nosso cotidiano, como:
-
O movimento do pêndulo ou oscilador no interior dos relógios de parede.
-
O pêndulo de Newton, cujas bolinhas descrevem um movimento oscilatório.
-
O movimento das molas de colchões, redes e balanços.
-
Os brinquedos decorativos colocados no interior do carro que oscilam no menor movimento, por serem feitos de mola.
-
O bater das assas dos pássaros ocorre de maneira rítmica, como um movimento oscilatório.
-
Quando pulamos corda, ela é batida em um padrão oscilatório.
Período do movimento oscilatório
O período do movimento oscilatório é definido como o tempo levado para concluir uma oscilação ou ciclo, sua unidade de medida é o segundo. Ele é calculado pela fórmula:
\(T=\frac{∆t}n\)
-
T → período de oscilação, medido em segundos \( \).
-
\(∆t\) → variação de tempo, medida em segundos \( \).
-
n → número de oscilações.
O período do movimento oscilatório é considerado o inverso da frequência do movimento oscilatório, definida como a quantidade de oscilações por tempo, e é calculado pela fórmula:
\(T=\frac{1}f\)
-
T → período de oscilação, medido em segundos \( \).
-
f → frequência de oscilação, medida em Hertz \( \).
O período do movimento oscilatório também pode ser calculado pela fórmula da velocidade angular:
\(ω=\frac{2π}T\)
-
ω → velocidade angular, medida em \([rad/s] \).
-
T → período de oscilação, medido em segundos \( \).
A frequência também pode ser calculada pela fórmula da velocidade angular:
\(ω=2\cdot π\cdot f\)
-
ω → velocidade angular, medida em \([rad/s] \).
-
f → frequência de oscilação, medida em Hertz \( \).
Fórmulas do movimento oscilatório
O movimento oscilatório pode ser descrito pelas função horária da posição do MHS, função horária da velocidade do MHS e função horária da aceleração do MHS.
→ Função horária da posição do movimento harmônico simples (MHS)
\(x(t)=A\cdot cos(ωt+ϕ)\)
-
\(x(t)\) → posição em função do tempo, medida em metros \( \).
-
A → amplitude da onda, medida em metros \( \).
-
\(ωt+ϕ\) → fase do movimento.
-
ω → velocidade angular, medida em \([rad/s] \).
-
t → tempo, medido em segundos \( \).
-
\(ϕ\) → constante de fase.
Exemplo:
Qual a função horária da posição de um oscilador harmônico que apresenta amplitude de 4 metros, velocidade angular de 2 rad/s e constante de fase igual a π?
Resolução:
A função horária da posição de oscilador harmônico é dada pela fórmula:
\(x(t)=A\cdot cos (ωt+ϕ)\)
Substituindo os valores dados no enunciado, obteremos a função para esse caso:
\(x(t)=4\cdot cos(2t+π)\)
→ Função horária da velocidade do movimento harmônico simples (MHS)
\(v(t)=-ω\cdot A\cdot sin(ωt+ϕ)\)
-
\(v(t)\) → velocidade em função do tempo, medida em metros \([m/s] \).
-
A → amplitude da onda, medida em metros \( \).
-
\(ωt+ϕ\) → fase do movimento.
-
ω → velocidade angular, medida em \([rad/s] \).
-
t → tempo, medido em segundos \( \).
-
\(ϕ\) → constante de fase.
Exemplo:
Qual a função horária da velocidade de um oscilador harmônico que apresenta amplitude de 1,5 m, velocidade angular de 0,2 rad/s e constante de fase igual a \(\frac{π}3 \)?
Resolução:
A função horária da velocidade de oscilador harmônico é dada pela fórmula:
\(v(t)=-ω\cdot A\cdot sin(ωt+ϕ)\)
Substituindo os valores dados no enunciado, obteremos a função para esse caso:
\(v(t)=- 0,2\cdot 1,5\cdot sin(0,2\cdot t+\frac{π}3)\)
\(v(t)=- 0,3\cdot sin(0,2t+\frac{π}3)\)
→ Função horária da aceleração do movimento harmônico simples (MHS)
\(a(t)=ω^2\cdot A\cdot cos(ωt+ϕ)\)
-
\(a(t)\) → aceleração em função do tempo, medida em metros \([m/s^2] \).
-
A → amplitude da onda, medida em metros \( \).
-
\(ωt+ϕ\) → fase do movimento.
-
ω → velocidade angular, medida em \([rad/s] \).
-
t → tempo, medido em segundos \( \).
-
\(ϕ\) → constante de fase.
A aceleração máxima é dada pela equação:
\(a(t)=ω^2\cdot x(t)\)
-
\(a(t)\) → aceleração em função do tempo, medida em metros \([m/s^2] \).
-
ω → velocidade angular, medida em \([rad/s] \).
-
\(x(t)\) → posição em função do tempo, medida em metros \( \).
Exemplo:
Qual a função horária da aceleração de um oscilador harmônico que apresenta amplitude de 3 m, velocidade angular de 8 rad/s e constante de fase igual a 2π?
Resolução:
A função horária da aceleração de oscilador harmônico é dada pela fórmula:
\(a(t)=ω^2\cdot A\cdot cos(ωt+ϕ)\)
Substituindo os valores dados no enunciado, obteremos a função para esse caso:
\(a(t)=8^2\cdot 3\cdot cos(8\cdot t+2π)\)
\(a(t)=192\cdot cos(8t+2π)\)
Veja também: Quais são as funções horárias que descrevem o movimento de queda livre?
Exercícios resolvidos sobre movimento oscilatório
Questão 1
Um pêndulo se locomove com uma velocidade angular de \(π/4\ rad/s\). Com base nisso, encontre a sua frequência de oscilação.
A) 0,125 Hz
B) 0,250 Hz
C) 0,500 Hz
D) 1,000 Hz
E) 2,000 Hz
Resolução:
Alternativa A
Calcularemos a frequência do movimento pela fórmula da velocidade angular:
\(v=2\cdot π\cdot f\)
\(\frac{π}4=2\cdot π\cdot f\)
\(f=\frac{π}4\cdot \frac{1}{2\cdot π}\)
\(f=\frac{1}8\)
\(f=0,125\ Hz\)
Questão 2
(Osec) Um móvel executa um movimento harmônico simples de equação
\(x(t)=8\cdot cos(\frac{π}{8\cdot t})\)
Onde t é dado em segundos e x em metros. Após 2,0 s, a elongação do movimento é:
A) zero
B) 2,0 m
C) 3,5 m
D) 5,7 m
E) 8,0 m
Resolução:
Alternativa D
A elongação do movimento é encontrada quando igualamos o tempo a 2 segundos na sua equação:
\(x(t)=8\cdot cos(\frac{π}{8\cdot t})\)
\(x(t)=8\cdot cos(\frac{π}{8\cdot2})\)
\(x(t)=8\cdot cos(\frac{π}{4})\)
\(x(t)=8\cdot cos(0,25\cdot π)\)
\(x(t)=8\cdot 0,707\)
\(x(t)=5,7\ m\)
Por Pâmella Raphaella Melo
Professora de Física