Ondas estacionárias

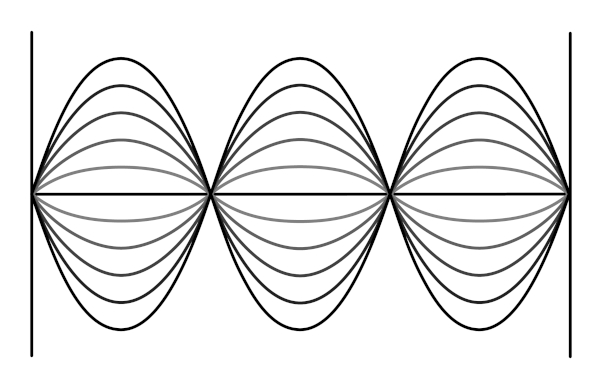
     As ondas estacionárias são formadas quando duas ondas, propagando-se em direções opostas, encontram-se. As ondas estacionárias são facilmente encontradas em instrumentos musicais de sopro e de corda, já que possuem barreiras que proporcionam a reflexão da onda.

Essas ondas, como qualquer onda, possuem: amplitude (A), comprimento de onda (λ), frequência (f) e velocidade (v). Além de possuírem os nós, nos quais ocorrem interferência destrutiva, e os ventres, nos quais ocorre interferência construtiva.

Cada crista ou vale nos dá o valor do harmônico, e, por meio da equação fundamental da onda (v = f . λ), é possível achar a velocidade, frequência e o comprimento da onda estacionária em cordas e tubos abertos ou fechados.

Veja também: 5 coisas que você precisa saber sobre as ondas sonoras

Tópicos deste artigo

• 1 - Resumo sobre ondas estacionárias
• 2 - Principais características das ondas estacionárias
• 3 - Velocidade das ondas estacionárias
• 4 - Ondas estacionárias em tubos sonoros
• 5 - Como calcular ondas estacionárias?
• 6 - Exercícios resolvidos sobre ondas estacionárias

Resumo sobre ondas estacionárias

• São o fenômeno que ocorre quando duas ondas, propagando-se em direções opostas, encontram-se.

• Normalmente aparecem em cordas ou tubos abertos ou fechados.

• Como qualquer onda, possuem: amplitude (A), comprimento de onda (λ), frequência (f) e velocidade (v). Além de possuírem os nós e ventres.

• Para achar sua velocidade, basta utilizar a equação fundamental da onda: v = f . λ.

• Nas cordas, o comprimento de onda em uma onda estacionária é metade do comprimento de onda total.

• Nos tubos fechados, o comprimento de onda em uma onda estacionária é um quarto do comprimento de onda total.

Principais características das ondas estacionárias

A onda estacionária é um fenômeno que ocorre quando duas ondas, propagando-se em sentidos contrários, interferem-se. Esse processo é causado pela ressonância (quando se aplica uma frequência igual ou próxima à do sistema), e, com isso, produz-se notas musicais em instrumentos de corda e sopro, o que é chamado de harmônico.

Na formação de uma onda estacionária, é possível observar um padrão em que há pontos de interferência destrutiva (diminuição de amplitude), nos quais não há movimentação, chamados de nós.

Além disso, pode-se observar pontos em que há a formação de cristas e vales (ponto mais alto e mais baixo da onda), nos quais há interferência construtiva (aumento de amplitude), e são conhecidos como antinós ou ventres.

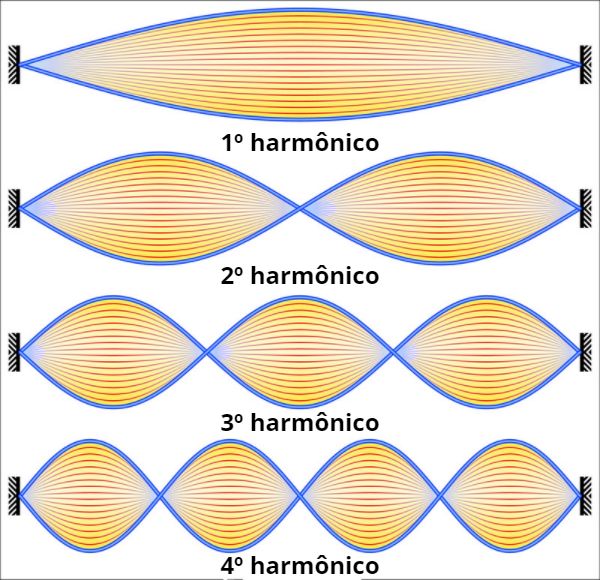
Cada crista ou vale pode ser contado para achar-se a ordem do harmônico, que necessariamente tem que ser um número inteiro. O 1º harmônico é a menor frequência que a onda pode ter e é chamado de harmônico fundamental.

Veja também: 5 coisas que você precisa saber sobre ondas

Velocidade das ondas estacionárias

A onda estacionária, assim como qualquer onda, possui uma velocidade conhecida por meio da equação fundamental da onda:

v = f . λ

v → velocidade da onda (m/s)

f → frequência da onda (Hz)

λ → comprimento de onda (m)

Quando a onda estacionária está sendo formada em uma corda uniforme, é possível encontrar a velocidade por meio da densidade da corda e a tensão sofrida por ela:

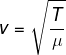
v → velocidade da onda (m/s)

T → tensão na corda (N)

µ → densidade linear de massa (kg/m³)

Ondas estacionárias em tubos sonoros

Além das cordas, as ondas estacionárias podem ser formadas quando o ar passa por tubos sonoros, abertos ou fechados, formando sons intensos, como em instrumentos de sopro.

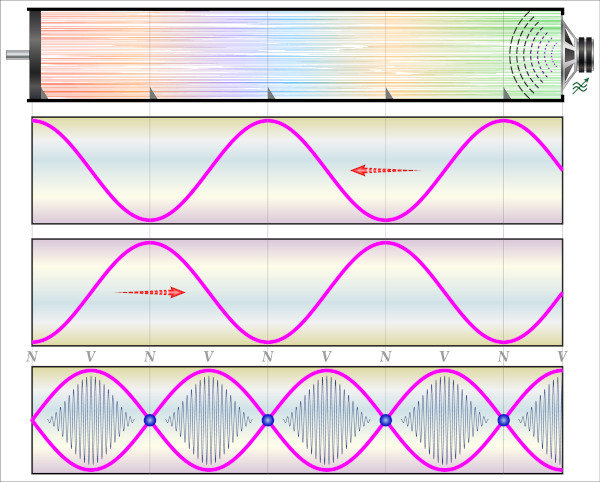
Nos tubos abertos, com as extremidades livres, as ondas estacionárias são produzidas com os ventres nas extremidades e os nós ao longo do seu interior.

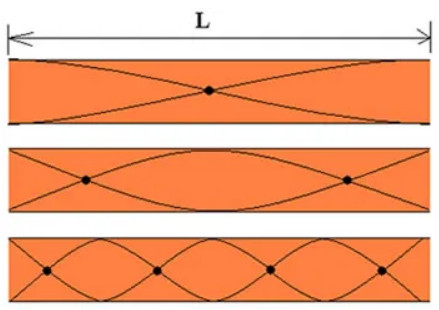
Nos tubos fechados, com uma das extremidades fechada e a outra livre, o nó é formado na sua extremidade fechada e ao longo do tubo, e o ventre é formado na sua extremidade aberta.

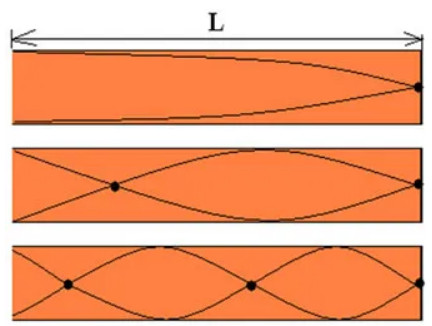
Como calcular ondas estacionárias?

A onda estacionária, em seu harmônico fundamental, apresenta uma formação diferente de uma onda, isso porque estamos vendo apenas metade da onda.

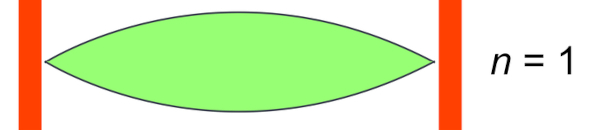
Dessa forma, o comprimento de onda de uma onda estacionária é encontrado após três nós consecutivos ou dois ventres.

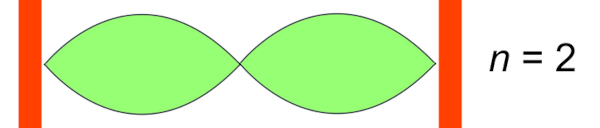
Uma forma de encontrar o harmônico é contando a quantidade de ventres que aparecem e vice-versa. Assim, o comprimento da corda para que ocorra uma onda estacionária deve ser um múltiplo inteiro (n = 1, 2, 3...) da metade do comprimento de onda (λ). Da seguinte maneira, conseguimos relacionar o comprimento de onda com o tamanho da corda:

L → comprimento da corda (m)

n → ordem do harmônico

λ → comprimento de onda (m)

Em tubos abertos, o comprimento do tubo pode ser encontrado pela mesma equação da corda. Agora, para achar a frequência dessa onda, utilizaremos a equação fundamental da onda, isolando a frequência:

v = f . λ

Sabendo que o comprimento de onda no harmônico fundamental é metade do comprimento total, e utilizando a equação do comprimento do tubo/corda:

Substituindo na equação fundamental:

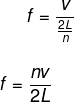
Em tubos fechados, a ordem dos harmônicos é dada por um múltiplo inteiro ímpar (n = 1, 3, 5…), e, pelo formato da onda, é visto que a distância entre um ventre e um nó consecutivos é igual a um quarto do comprimento de onda. Assim, para achar o comprimento do tubo e a frequência da onda, precisamos alterar o 2 pelo 4:

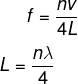
Leia mais: Ondas de rádio – ondas eletromagnéticas muito utilizadas nas telecomunicações

Exercícios resolvidos sobre ondas estacionárias

Questão 1 - (Uece 2017) Uma corda de 60 cm, em um violão, vibra a uma determinada frequência. É correto afirmar que o maior comprimento de onda dessa vibração, em cm, é:

A) 60

B) 120

C) 30

D) 240

Resolução

Alternativa B

O maior comprimento de onda é dado na menor frequência, vista no harmônico fundamental (n = 1). Assim, com as informações do enunciado e sabendo que a onda é formada em uma corda:

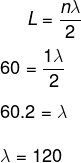
Questão 2 - (Enem 2016) Um experimento para comprovar a natureza ondulatória da radiação de micro-ondas foi realizado da seguinte forma: anotou-se a frequência de operação de um forno de micro-ondas e, em seguida, retirou-se sua plataforma giratória. No seu lugar, colocou-se uma travessa refratária com uma camada grossa de manteiga. Depois disso, o forno foi ligado por alguns segundos. Ao se retirar a travessa refratária do forno, observou-se que havia três pontos de manteiga derretida alinhados sobre toda a travessa. Parte da onda estacionária gerada no interior do forno é ilustrada na figura.

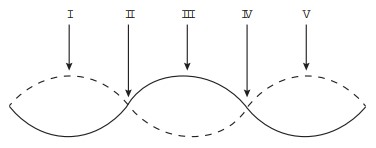
De acordo com a figura, que posições correspondem a dois pontos consecutivos da manteiga derretida?

A) I e III

B) I e V

C) II e III

D) II e IV

E) II e V

Resolução

Alternativa A. O aquecimento ocorrerá onde a interferência da onda foi construtiva, onde tiver maior intensidade, que é a região de vales e cristas (ponto mais alto e mais baixo da onda). Essa região é apresentada nos ventres das ondas: pontos consecutivos I e III ou III e V.

Por Gabriela de Oliveira
Professora de Física