Movimento harmônico simples

O movimento harmônico simples (MHS) é um movimento periódico que acontece exclusivamente em sistemas conservativos – aqueles em que não há ação de forças dissipativas. No MHS, uma força restauradora atua sobre o corpo de modo a fazê-lo voltar sempre a uma posição de equilíbrio. A descrição do MHS é feita com base nas grandezas frequência e período, por meio de funções horárias do movimento.

Veja também: Ressonância – entenda de uma vez esse fenômeno físico!

Tópicos deste artigo

• 1 - Resumo sobre MHS
• 2 - Equações do MHS
  • → Equação da posição no MHS
  • → Equação da velocidade no MHS
  • → Equação da aceleração no MHS
• 3 - Oscilador massa-mola
• 4 - Pêndulo simples
• 5 - Energia mecânica no MHS
• 6 - Exercícios sobre movimento harmônico simples

Resumo sobre MHS

Todo MHS acontece quando uma força impele um corpo em movimento a voltar para uma posição de equilíbrio. Alguns exemplos de MHS são o pêndulo simples e o oscilador massa-mola. Em movimento harmônico simples, a energia mecânica do corpo é sempre mantida constante, mas suas energia cinética e potencial intercambiam-se: quando a energia cinética é máxima, a energia potencial é mínima e vice-versa.

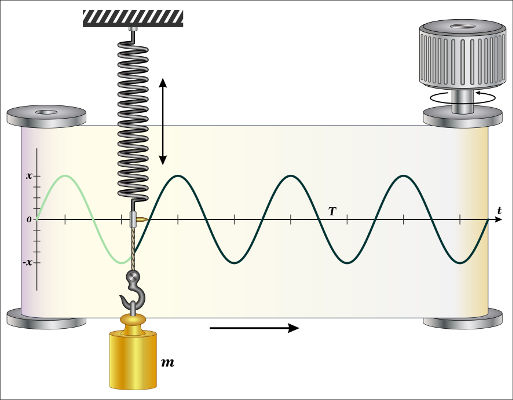
As grandezas mais importantes no estudo do MHS são aquelas que são usadas para escrever as funções horárias do MHS. As funções horárias nada mais são que equações que dependem do tempo como variável. Confira as principais grandezas do MHS:

• mede a maior distância que o corpo em oscilação é capaz de chegar em relação à posição de equilíbrio. A unidade de medida da amplitude é o metro (m);Amplitude (A):

• Frequência (f): mede a quantidade de oscilações que o corpo realiza a cada segundo. A unidade de medida da frequência é o hertz (Hz);

• Período (T): tempo necessário para que o corpo realize uma oscilação completa. A unidade de medida do período é o segundo (s);
• Frequência angular (ω): mede a rapidez em que o ângulo de fase é percorrido. O ângulo de fase corresponde à posição do corpo em oscilação. Ao final de uma oscilação, o corpo terá varrido um ângulo de 360º ou 2π radianos.

ω – frequência ou velocidade angular (rad/s)

Δθ – variação do ângulo (rad)

Equações do MHS

Vamos conhecer as equações gerais do MHS, começando pelas equações de posição, velocidade e aceleração.

→ Equação da posição no MHS

Esta equação é usada para calcular a posição do corpo que desenvolve um movimento harmônico simples:

x(t) – posição em função do tempo (m)

A – amplitude (m)

ω – frequência angular ou velocidade angular (rad/s)

t – tempo (s)

φ₀ – fase inicial (rad)

→ Equação da velocidade no MHS

A equação da velocidade do MHS deriva da equação horária da posição e é dada pela expressão a seguir:

→ Equação da aceleração no MHS

A equação da aceleração é bastante parecida com a equação da posição:

Além das equações mostradas acima, que são gerais, existem algumas equações específicas, utilizadas para calcular a frequência ou o período dos osciladores massa-mola e também do pêndulo simples. A seguir, explicaremos cada uma dessas fórmulas.

Veja também: Queda livre: o que é, exemplos, fórmulas, exercícios

Oscilador massa-mola

No oscilador massa-mola, um corpo de massa m é preso a uma mola ideal de constante elástica k. Quando retirado da posição de equilíbrio, a força elástica exercida pela mola faz com que o corpo passe a oscilar em torno dessa posição. A frequência e o período de oscilação podem ser calculados por meio das fórmulas a seguir:

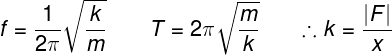
k – constante elástica da mola (N/m)

m – massa do corpo

Analisando a fórmula acima, é possível notar que a frequência de oscilação é proporcional à constante elástica da mola, ou seja, quanto mais “dura” for a mola, mais rápido será o movimento de oscilação do sistema massa-mola.

Pêndulo simples

O pêndulo simples consiste em um corpo de massa m, preso a um fio ideal e inextensível, colocado para oscilar em ângulos pequenos, na presença de um campo gravitacional. As fórmulas utilizadas para calcular a frequência e o período desse movimento são as seguintes:

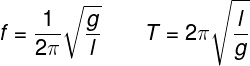
g – aceleração da gravidade (m/s²)

l – comprimento do fio (m)

A partir das equações acima, percebe-se que o período do movimento de um pêndulo depende apenas do módulo da gravidade local e também do comprimento desse pêndulo.

Energia mecânica no MHS

O movimento harmônico simples só é possível graças à conservação da energia mecânica. A energia mecânica é a medida da soma da energia cinética e da energia potencial de um corpo. No MHS, a todo momento, tem-se a mesma energia mecânica, entretanto, ela se expressa periodicamente na forma de energia cinética e energia potencial.

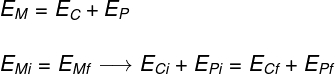
E_M – energia mecânica (J)

E_C – energia cinética (J)

E_P – energia potencial (J)

A fórmula mostrada acima expressa o sentido matemático da conservação da energia mecânica. Em um MHS, em quaisquer instantes, final e inicial, por exemplo, a soma das energias cinética e potencial é equivalente. Esse princípio pode ser visualizado no caso do pêndulo simples, que apresenta energia potencial gravitacional máxima, quando o corpo se encontra nas posições extremas, e energia cinética máxima, quando o corpo se encontra no ponto mais baixo da oscilação.

Exercícios sobre movimento harmônico simples

Questão 1) Um corpo de 500 g é amarrado a um pêndulo simples de 2,5 m e é colocado para oscilar em uma região onde a gravidade é igual a 10 m/s². Determine o período de oscilação desse pêndulo em função de π.

a) 2π/3 s

b) 3π/2 s

c) π s

d) 2π s

e) π/3 s

Gabarito: letra C. O exercício pede que calculemos o período do pêndulo simples, para isso devemos usar a fórmula a seguir. Confira como é feito o cálculo:

e acordo com o cálculo realizado, o período de oscilação desse pêndulo simples é igual a π segundos.

Questão 2) Um objeto de 0,5 kg está preso a uma mola de constante elástica de 50 N/m. Com base nos dados, calcule, em hertz e em função de π, a frequência de oscilação desse oscilador harmônico.

a) π Hz

b) 5π Hz

c) 5/π Hz

d) π/5 Hz

e) 3π/4 Hz

Gabarito: letra C. Vamos usar a fórmula da frequência do oscilador massa-mola:

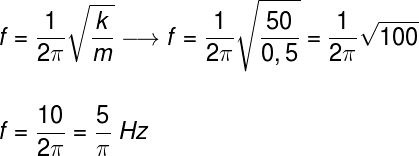
Fazendo o cálculo acima, descobrimos que a frequência de oscilação desse sistema é de 5/ π Hz.

Questão 3) A função horária da posição de um oscilador harmônico qualquer é mostrada a seguir:

Assinale a alternativa que indica corretamente a amplitude, a frequência angular e a fase inicial desse oscilador harmônico:

a) 2π m; 0,05 rad/s; π rad.

b) π m; 2 π rad/s, 0,5 rad.

c) 0,5 m; 2 π rad/s, π rad.

d) 1/2π m; 3π rad/s; π/2 rad.

e) 0,5 m; 4π rad/s; π rad.

Gabarito: letra C. Para resolvermos o exercício, basta que o relacionemos com a estrutura da equação horária do MHS. Observe:

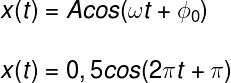
Ao compararmos as duas equações, percebemos que a amplitude é igual a 0,5 m, a frequência angular é igual a 2π rad/s e a fase inicial é igual a π rad.

 

Por Rafael Helerbrock
Professor de Física