Onda periódica e sua equação

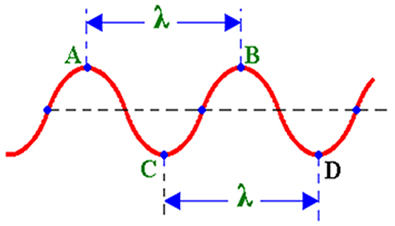
Nos estudos sobre ondas, definimos ondas periódicas como sendo as ondas geradas por fontes oscilantes, ou seja, são ondas que se repetem em intervalos de tempos iguais. Na figura acima temos a representação básica de uma onda periódica que se propaga em uma corda tensionada. Podemos ver também que apresentamos alguns elementos básicos que a ela estão associados, como, por exemplo, as cristas e o comprimento da onda, os vales e a amplitude da onda.

Vamos agora considerar a figura abaixo, onde temos uma corda tensionada, ou seja, totalmente esticada. Na figura, podemos identificar como sendo o ponto F a fonte emissora de ondas; e o ponto O como sendo a origem.

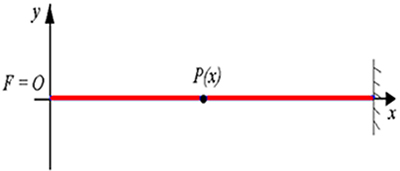
Tomando por base a situação acima, vamos considerar o tempo igual a zero (t = 0). Nesse caso, o ponto F executará um movimento harmônico simples cuja amplitude vale A e a fase inicial θ₀, de modo que a ordenação y de F variará com o tempo. Seguindo a equação do MHS, temos:

y=A.cos⁡ (ω.t+ θ₀ )

Caso não ocorra dissipação de energia durante a propagação da onda, podemos dizer que, após certo intervalo de tempo (Δt), o ponto P situado no meio da corda passa a descrever ummovimento harmônico simples com o mesmo valor da amplitude A, porém atrasado Δt em relação a F.

Como Δt é o intervalo de tempo que a onda levou para atingir P, temos:

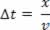
Na equação acima, x é a abscissa do ponto P e v é a velocidade com que a onda se propaga na corda. Vejamos a figura abaixo:

Assim, o ponto genérico P tem sua ordenada, y, dada em função do tempo por:

y=A.cos[ω.(t-∆t)+θ₀ ]

Lembrando que ω = 2πf e que Δt = x/v, temos:

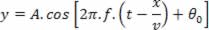
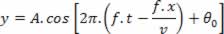
Substituindo 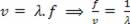, segue:

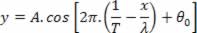
Para cada ponto da corda, a abscissa x é fixa e a ordenada y varia em função do tempo, de acordo com essa função.

Por Domiciano Marques
Graduado em Física