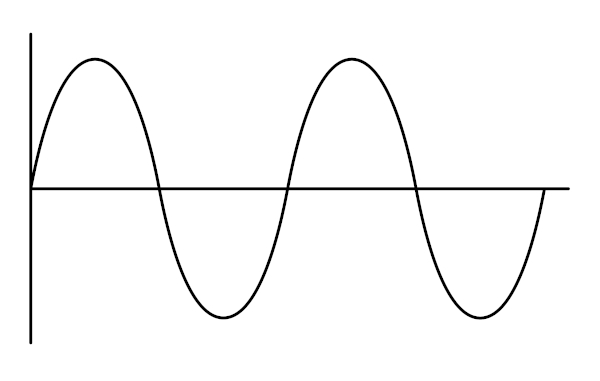
As ondas periódicas são formadas por pulsos com período constante. Embora a perturbação do meio seja propagada por ele todo, se selecionarmos um único ponto da onda, perceberemos que ele permanecerá no mesmo local durante o movimento. Como qualquer onda, as periódicas possuem crista, vale, frequência, comprimento de onda, período e velocidade de propagação.
Leia também: 5 coisas que você precisa saber sobre ondas
Tópicos deste artigo
- 1 - Resumo sobre ondas periódicas
- 2 - O que são ondas periódicas?
- 3 - Classificação das ondas periódicas
- 4 - Elementos das ondas periódicas
- 5 - Fórmulas das ondas periódicas
- 6 - Comprimento de onda
- 7 - Exercícios resolvidos sobre ondas periódicas
Resumo sobre ondas periódicas
-
Ondas periódicas possuem período constante.
-
Período é o intervalo de tempo de um pulso completar uma oscilação.
-
As características dessas ondas são: amplitude (crista e vale), comprimento de onda, frequência, período e velocidade de propagação.
-
Os pontos das cristas e dos vales oscilam em oposição de fase entre si.
-
Os pontos das cristas oscilam em concordância de fase.
-
Os pontos dos vales oscilam em concordância de fase.
-
A frequência e o período se relacionam pelo inverso um do outro.
-
Com a equação fundamental da ondulatória, é possível encontrar a velocidade de propagação da onda: v = λ . f.
O que são ondas periódicas?
As ondas periódicas são perturbações no meio provocadas por uma fonte com período constante, ou seja, o intervalo para completar um pulso ou uma oscilação é um valor constante.
Classificação das ondas periódicas
Como qualquer onda, as ondas periódicas podem ser classificadas em relação a sua natureza, direção de propagação e de vibração.
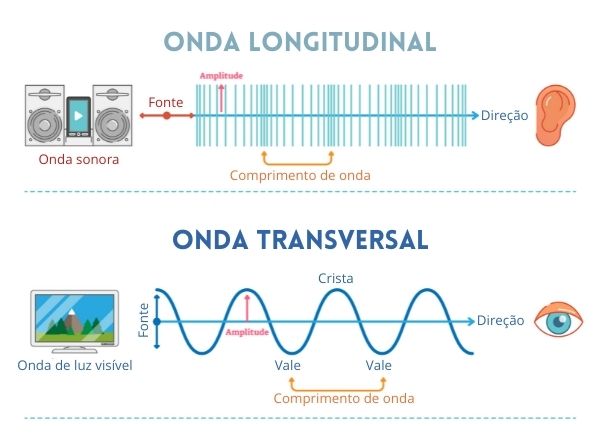
→ Classificação das ondas periódicas quanto à natureza
-
Mecânica: ondas que precisam de um meio para se propagar, como a onda do mar e a onda sonora.
-
Eletromagnética: ondas que não precisam de um meio material para se propagar, como a luz.
→ Classificação das ondas periódicas quanto à direção de propagação
-
Unidimensional: ondas que se propagam em apenas uma direção, como um pulso em uma corda.
-
Bidimensional: ondas que se propagam em duas dimensões, como ondas na superfície de uma piscina.
-
Tridimensional: ondas que se propagam em todas as direções, como a onda sonora.
→ Classificação das ondas periódicas quanto à direção de vibração
-
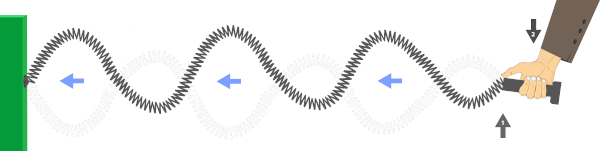
Longitudinal: ondas que possuem a direção de vibração da fonte igual à direção de propagação da onda, como a onda sonora saindo de um equipamento de som.
-
Transversal: ondas que possuem a direção de vibração perpendicular à direção de propagação da onda, como a onda de uma corda.
Leia mais: Ondas estacionárias — formadas quando duas ondas, propagando-se em direções opostas, encontram-se
Elementos das ondas periódicas
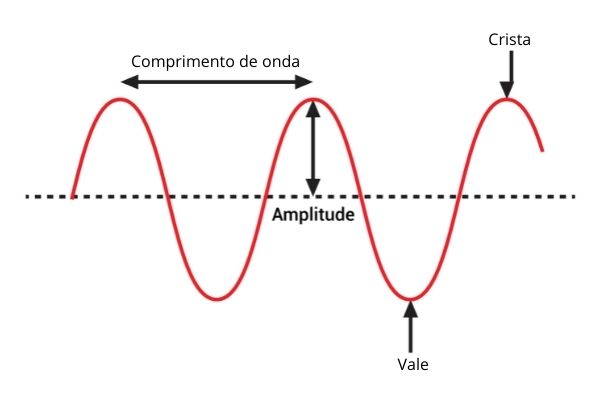
As ondas periódicas, como qualquer onda, possuem: amplitude (A), comprimento de onda (λ), frequência (f), período (T) e velocidade de propagação (v).
-
Amplitude (A): é a distância entre o eixo central e o ponto mais alto (crista) ou mais baixo da onda (vale). Sua unidade de medida no Sistema Internacional é o metro (m).
-
Comprimento de onda (λ): é a medida de um ciclo completo da onda, que pode ser medido entre duas cristas, dois vales ou entre uma crista e um vale. Sua unidade de medida no S.I. é o metro (m).
-
Frequência (f): é a quantidade de ciclos em um determinado intervalo de tempo. Se as cristas e os vales estão muito próximos, isso significa que a frequência da onda é alta, do contrário, a frequência é baixa. Sua unidade de medida no S.I. é o hertz (Hz).
-
Período (T): é o intervalo de tempo para se completar um ciclo de onda. Por isso, o período é medido no intervalo de um comprimento de onda. Sua unidade de medida no S.I. é o segundo (s).
-
Velocidade de propagação (v): muda dependendo do meio onde a onda está, e é dada pela equação fundamental da ondulatória: V = λ/T = λ . f. Sua unidade de medida no S.I. é o metro por segundo (m/s).
Fórmulas das ondas periódicas
Para encontrar o período ou a frequência de uma onda periódica, basta relacionar essas duas grandezas.
Para encontrar e frequência:
![]()
Para encontrar o período:
![]()
Para encontrar a velocidade de propagação de uma onda, basta utilizar a equação de velocidade na cinemática, que, adaptada para a ondulatória, é chamada de equação fundamental da ondulatória:
![]()
Substituindo o deslocamento linear pelo deslocamento da onda e o intervalo de tempo pelo período:
![]()
Comprimento de onda
O comprimento de onda é a distância de um ciclo de onda. Esse comprimento pode ser encontrado entre duas cristas, pontos mais altos da onda, ou entre dois vales, pontos mais baixos da onda.
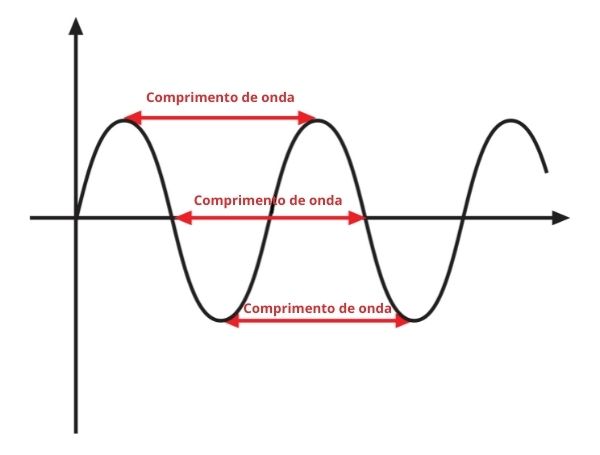
O comprimento de onda é medido em metros e representado pela letra grega λ. Os pontos mais altos, as cristas, vibram em concordância de fase. Os pontos mais baixos, os vales, também vibram em concordância. Contudo, as cristas e os vales vibram em oposição de fase entre si.
Exercícios resolvidos sobre ondas periódicas
Questão 1
(Mackenzie) O gráfico representa uma onda que se propaga com velocidade constante de 200 m/s. A amplitude (A), o comprimento de onda (λ) e a frequência (f) da onda são, respectivamente:
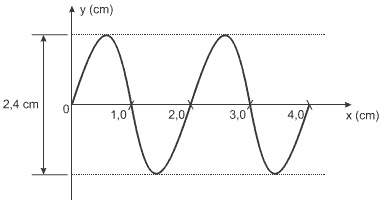
a) 2,4 cm; 1,0 cm; 40 kHz
b) 2,4 cm; 4,0 cm; 20 kHz
c) 1,2 cm; 2,0 cm; 40 kHz
d) 1,2 cm; 2,0 cm; 10 kHz
e) 1,2 cm; 4,0 cm; 10 kHz
Resolução:
Alternativa d
Como a amplitude é a distância do eixo central até uma das extremidades da onda (crista ou vale), então ela é dada pela metade do comprimento total vertical da onda.
![]()
Considerando a distância entre o início de uma crista e o final de um vale, o comprimento de onda (λ) = 2 cm.
Com a velocidade sendo 200 m/s, para encontrar a frequência, basta utilizar a equação fundamental da ondulatória, tomando cuidado com as unidades de medida:
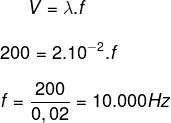
Questão 2
(Unesp) A propagação de uma onda no mar da esquerda para a direita é registrada em intervalos de 0,5 s e apresentada através da sequência dos gráficos da figura, tomados dentro de um mesmo ciclo:
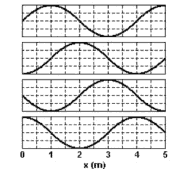
Analisando os gráficos, podemos afirmar que a velocidade da onda, em m/s, é de
a) 1,5.
b) 2,0.
c) 4,0.
d) 4,5.
e) 5,0.
Resolução
Alternativa b
Como o registro é feito da mesma onda em intervalos de 0,5 segundos, ao escolhermos um ponto da crista ou do vale, é possível determinarmos a velocidade do ponto.
Considerando o ponto mais alto no primeiro gráfico e depois no segundo gráfico, é possível perceber que a crista deslocou 1 metro em 0,5 segundos.
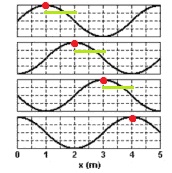
Assim, substituindo essas informações na equação fundamental da ondulatória:
![]()