A dilatação superficial é o fenômeno físico da termologia em que a área de um corpo pode sofrer variações por conta de uma mudança de temperatura, seja aquecimento, seja resfriamento. Matematicamente, a dilatação e a variação de temperatura são diretamente proporcionais entre si.
Todo corpo, de acordo com sua composição, tem um coeficiente de dilatação superficial, uma grandeza constante (em certos intervalos de temperatura). Quando a dilatação ocorre nas três dimensões (altura, largura e comprimento), é possível adaptar a fórmula para que descreva corretamente as variações observadas.
Leia também: Quais são os três tipos de dilatação térmica?
Tópicos deste artigo
- 1 - Resumo sobre dilatação superficial
- 2 - O que é dilatação superficial?
- 3 - Fórmula da dilatação superficial
- 4 - Como calcular a dilatação superficial?
- 5 - Coeficiente de dilatação superficial
- 6 - Dilatação superficial no dia a dia
- 7 - Dilatação superficial e volumétrica
- 8 - Experimento de dilatação superficial
- 9 - Exercícios resolvidos sobre dilatação superficial
Resumo sobre dilatação superficial
- Dilatação superficial é o fenômeno que relaciona a variação das dimensões de área de um corpo com a variação de temperatura.
- Para determinar matematicamente a dilatação superficial, usa-se \(\Delta S = S_0 \cdot \beta \cdot \Delta \theta \).
- Ao calcular a dilatação superficial, deve-se compreender a diferença entre o que será a variação de área e a área inicial antes da mudança de temperatura.
- O coeficiente de dilatação superficial é determinado pelo coeficiente de dilatação linear.
- No cotidiano é possível notar diversas tecnologias que são desenvolvidas levando em consideração a dilatação superficial, principalmente na construção civil.
- A diferença entre a dilatação superficial e volumétrica está no número de dimensões afetadas pelo aquecimento.
O que é dilatação superficial?
A dilatação superficial é o fenômeno físico associado à mudança de área de um corpo devido à variação de temperatura, seja de aquecimento, seja de resfriamento. Quando um corpo sofre uma variação de temperatura por meio da troca de calor, é possível notar mudanças físicas na sua estrutura material.
Os objetos, no mundo real, estão em três dimensões, pois têm largura, comprimento e altura. Porém, como um exercício teórico, pode-se determinar que a altura em alguns casos é um valor desprezível, pensando na ordem de grandeza das dimensões envolvidas, por exemplo, uma placa de azulejo, um tampo de madeira de mesa ou uma lâmina de vidro de janela.
Nessas situações, a mudança de tamanho causada por variações de temperatura recebe o nome de dilatação superficial. Variações de temperatura promovem mais (ou menos) movimento cinético das moléculas, com isso as mesmas moléculas ocuparão mais (ou menos) espaço físico.
Fórmula da dilatação superficial
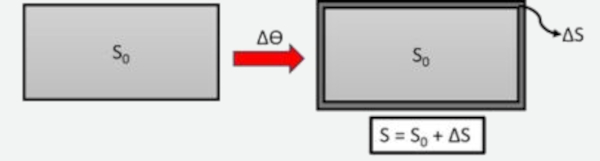
A dilatação superficial é descrita matematicamente pela seguinte fórmula:
\(\Delta S = S_0 \cdot \beta \cdot \Delta \theta \)
Em que:
\(\Delta S\) – Variação superficial (ou variação de área), medida em m² (e suas escalas).
\(\Delta \theta \) – Variação de temperatura, medida em °C.
\(S_0 \) – Superfície inicial (área inicial), medida em m² (e suas escalas).
\(\beta\) – Coeficiente de dilação superficial, medido em °C-1.
Veja também: Como ocorre a dilatação térmica nos líquidos
Como calcular a dilatação superficial?
Para calcular a dilatação superficial, deve-se levar em conta basicamente que o objetivo da fórmula é estimar a variação sofrida pelo corpo durante o aquecimento ou resfriamento, com base nas suas dimensões iniciais. A partir do momento que se obtém a variação superficial causada pela dilatação, pode-se chegar ao valor final.
Veja o exemplo:
Uma placa retangular de aço, de 2x2 metros de área, sofre um aquecimento de 70 °C. Sabendo que o coeficiente de dilatação linear do aço é 1,1 x 10-5 °C, determine a área da placa após sofrer a variação de temperatura. Como a placa de ação tem as dimensões 2x2, sua área inicial possui 4 m². Levando em consideração que a dilatação ocorre superficialmente, é preciso ajustar o valor do coeficiente de dilatação linear para o coeficiente de dilatação superficial.
Logo:
β = 2.α, assim β = 2,2 x 10-5 °C-1
Dessa maneira, ao aplicar a fórmula:
\(\Delta S = S_0 \cdot \beta \cdot \Delta \theta \quad \underrightarrow{logo} \quad \Delta S = 4\cdot 2,2 \times 10^{-5} \cdot 70 = 616 \times 10^{-5} \)
Ou seja, a variação de superfície sofrida é 6,16 x 10-3 m.
Logo, a superfície, ou área, no final do aquecimento será 4,000616 m.
Coeficiente de dilatação superficial
O coeficiente de dilatação de qualquer material representa matematicamente a constante de proporcionalidade entre a variação dimensional de um corpo e sua variação de temperatura. É habitualmente descrito em função da dilatação linear (α), a compreensão da variação do tamanho de apenas uma dimensão. No caso da dilatação superficial (β), que ocorre em duas dimensões, é preciso multiplicar o coeficiente por 2.
Veja:
|
Substância |
(α) em 10−6°C−1 |
(β) em 10−6°C−1 |
Faixa de temperaturas °C |
|
Prata |
20 |
40 |
100-390 |
|
Ouro |
14 |
28 |
100-390 |
|
Vidro |
8,6 |
17,2 |
20-300 |
Então, para qualquer substância, deve admitir que:
\(\beta = 2 \cdot \alpha\)
Dilatação superficial no dia a dia
No cotidiano é possível encontrar diversos exemplos de como a dilatação superficial é aplicada em diversas tecnologias, principalmente na construção civil. Diversas estruturas, como linhas de trem, pontes ou edifícios, são projetadas para ficarem em exposição prolongada ao Sol. Assim, é previsto que sofram diversas amplitudes diferentes de temperatura, sejam altas (de dia), sejam baixas (à noite).

Quando o concreto se aquece durante o dia pela exposição ao Sol, suas dimensões sofrerão uma consequente dilatação. Caso as placas de concreto fossem inteiriças, existiria o risco real de que elas se quebrassem, pois, ao aumentarem de tamanho o espaço que ocupam, esse espaço ainda seria limitado. As fendas de dilatação garantem o espaço adequado para que haja a dilatação com segurança. A mesma tecnologia pode ser encontrada em prédios, calçadas, pontes e pilastras.

Outro exemplo comum é ouvir estalos durante a noite nos móveis de casa ou nas janelas. Ao anoitecer, e com a esperada queda de temperatura, diversas placas de vidro, aço e madeira sofrerão um “encolhimento”, provocando estalos que comumente geram boatos de casas que estejam “assombradas”.
Dilatação superficial e volumétrica
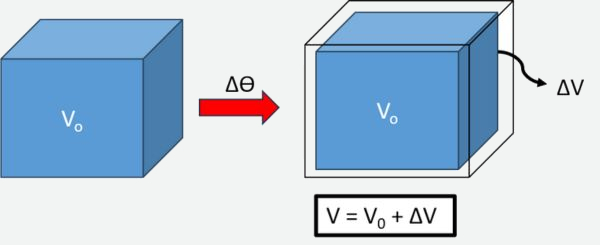
A diferença entre a dilatação superficial e volumétrica está no número de dimensões afetadas pelo aquecimento. Se a altura de um corpo não pode ser desprezada durante a variação de temperatura, a dilatação que esse corpo sofrerá será volumétrica. Nesse caso, é necessário adaptar a fórmula da dilatação superficial para que ela leve em consideração o coeficiente de dilatação volumétrica (γ), já que são as três dimensões do corpo que sofrerão a variação de tamanho.
Logo:
\(\gamma = 3\cdot α\)
Então a fórmula da dilatação volumétrica fica como:
\(\Delta V = V_0 \cdot \gamma \cdot \Delta \theta \)
\(\Delta V\) – Variação volumétrica, medida em m3(e suas escalas).
\(\Delta \theta \) – Variação de temperatura, medida em °C.
\(V_0\) – Volume inicial (área inicial), medido em m3 (e suas escalas).
\(\gamma\) – Coeficiente de dilação volumétrica, medido em °C-1.
→ Dilatação superficial e volumétrica
Experimento de dilatação superficial
Para verificar experimentalmente a existência da dilatação superficial, é possível construir uma prática bem simples. Para isso é necessário:
- 1 placa de isopor plana
- 1 moeda
- 1 alicate
- 1 caneta
- 1 vela
Comece colocando a moeda sobre o isopor e faça, com a caneta, uma marca do contorno da moeda. Usando uma tesoura, recorte o espaço demarcado e faça um orifício na placa do diâmetro da moeda. Usando o alicate, segure a moeda por alguns instantes na vela. Ao sentir que ela aqueceu bem, tente aproximar do orifício e perceba como a área circular da moeda não permitirá que ela se encaixe.
Espere a moeda resfriar. Use água corrente da torneira para ajudar. Tente mais uma vez encaixar a moeda no orifício e perceba que, na temperatura mais baixa, ela passará perfeitamente.
Saiba mais: Dilatação real x dilatação aparente — qual a diferença?
Exercícios resolvidos sobre dilatação superficial
1. (Uerj) Em um instituto de análises físicas, uma placa de determinado material passa por um teste que verifica o percentual de variação de sua área ao ser submetida a aumento de temperatura. Antes do teste, a placa, que tem área igual a 3,0×103cm2, encontra-se a 20 °C; ao ser colocada no forno, sua temperatura atinge 60 °C. Sabe-se que o coeficiente de dilatação linear do material que a constitui é igual a 1,5×10-5°C-1.
Nesse teste, o percentual de variação da área da placa foi de:
a) 0,16%
b) 0,12%
c) 0,8%
d) 0,6%
Resposta:
Aplicando a fórmula da dilatação superficial, temos que a variação percentual da área foi de:
\(\Delta S = S_0\beta \Delta \theta\\ \frac{\Delta S}{S_0} = 2 \cdot 1,5\cdot 10^{-5}\cdot (60-20)\\ \frac{\Delta S}{S_0} = 3\cdot 10^{-5}\cdot 40\\ \frac{\Delta S}{S_0} = 120\cdot 10^{−5}=0,0012 \cdot 100 \% \\ \frac{\Delta S}{S_0} = 0,12 \%\)
2. (Mackenzie) Uma placa de alumínio (coeficiente de dilatação linear do alumínio 2⋅10-5°C-1, com 2,4 m2 de área a temperatura de -20 °C, foi aquecido em 176 °F. O aumento de área da placa foi de:
a) 24 cm2
b) 48 cm2
c) 96 cm2
d) 120 cm2
e) 144 cm2
Resposta:
Dados: α = 2 x 10-5°C-1; A0 = 2,4 m2; T0 = -20 °C; T = 176 °F.
Usando a equação de conversão de °F para °C:
\(\frac{T_C}{5} = \frac{T_F - 32}{9} \Rightarrow \frac{T_C}{5} = \frac{176 - 32}{9} \Rightarrow T_C = 80\ ^\circ\text{C} \)
Aplicando a expressão da dilatação superficial:
\(\Delta S = S_0 \, \beta \, \Delta T = S_0 \cdot 2\alpha (T_C - T_0) \\ \Delta S = 2{,}4 \cdot (2 \cdot 2 \cdot 10^{-5}) \cdot [80 - (-20)] \\ \Delta S = 2{,}4 \cdot (4 \cdot 10^{-5}) \cdot 100 \\ \Delta S = 9{,}6 \cdot 10^{-3} \ \text{m}^2 \Rightarrow \Delta S = 96 \ \text{cm}^2 \)
Fontes
HALLIDAY, D.; RESNICK, R.; WALKER, J. (colab.). Fundamentos de física: gravitação, ondas e termodinâmica, volume 2. 10. ed. Rio de Janeiro: LTC - Livros Técnicos e Científicos, 2016.
HEWITT, P. G. Física conceitual. 9. ed. Porto Alegre: Bookman, 2002.
SOUZA, L. F. de. Um experimento sobre a dilatação térmica e a lei de resfriamento. Monografia de Conclusão de Curso, Instituto de Física - UFRJ, Maio 2007.


