Dilatação dos líquidos

Os líquidos podem sofrer dilatação térmica, assim como os sólidos, quando aquecidos. A dilatação dos líquidos ocorre quando sua temperatura aumenta, de forma que suas moléculas fiquem mais agitadas. Para determinarmos a dilatação do volume de um líquido, precisamos conhecer o seu coeficiente de dilatação volumétrica, mas, também, deve-se levar em conta a dilatação sofrida pelo recipiente que contém esse líquido.

A dilatação sofrida pelos líquidos é chamada de dilatação volumétrica. Nesse tipo de dilatação, todas as dimensões de um corpo ou fluido, como líquidos e gases, sofrem aumentos significativos em resposta a um aumento de temperatura. Tal fenômeno surge em razão da agitação térmica das moléculas do corpo: quanto maior a temperatura, maior é a amplitude da agitação dessas moléculas, que passam a deslocar-se em um espaço maior.

Veja também: Conceitos básicos da Hidrostática

Tópicos deste artigo

• 1 - Fórmula da dilatação volumétrica
• 2 - Coeficiente de dilatação volumétrica
• 3 - Dilatação aparente dos líquidos
  • Fórmulas da dilatação aparente
• 4 - Dilatação anômala da água
• 5 - Exercícios resolvidos sobre dilatação dos líquidos

Fórmula da dilatação volumétrica

Podemos calcular a dilatação volumétrica sofrida por um líquido por meio da seguinte fórmula:

ΔV — variação de volume (m³)

V₀ — volume inicial (m³)

γ — coeficiente de dilatação volumétrica (ºC^-1)

ΔT — variação de temperatura (ºC)

A fórmula mostrada acima pode ser usada para calcular o aumento no volume (ΔV) de um líquido em razão de uma variação em sua temperatura (ΔT). Com algumas manipulações algébricas, é possível escrever a mesma fórmula anterior em um formato que nos permite calcularmos diretamente o volume final de um líquido após o seu aquecimento, confira:

V — volume final do líquido

Perceba que, em ambas as fórmulas, é necessário que se conheça o quanto vale a constante γ, conhecida como coeficiente de dilatação volumétrica. Essa grandeza, medida em ºC^-1(lê-se: 1 sobre graus Celsius), fornece-nos quão grande é a dilatação de alguma substância, para cada 1ºC de variação em sua temperatura.

Coeficiente de dilatação volumétrica

O coeficiente de dilatação volumétrica é uma propriedade física que mede quão grande é a variação de volume de um corpo, para uma dada mudança em sua temperatura. Essa grandeza não é constante, e o seu valor pode ser considerado constante para somente alguns intervalos de temperatura. Confira alguns valores típicos dos coeficientes de dilatação de algumas substâncias no estado líquido, à temperatura de 20 ºC:

Como dito anteriormente, o coeficiente de dilatação volumétrica tem dependência com a temperatura, ou seja, seu módulo pode variar durante um aquecimento ou resfriamento. Por isso, para fazermos os cálculos, utilizamos os coeficientes de dilatação que se encontrem dentro dos intervalos de temperatura, em que o gráfico de V x T tenha o formato linear. Observe:

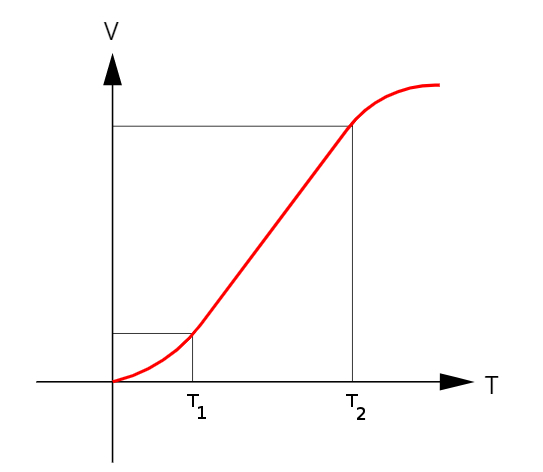
Entre as temperaturas T₁ e T₂, o coeficiente de dilatação é constante.

Dilatação aparente dos líquidos

A dilatação aparente dos líquidos é determinada pelo volume de líquido que é transbordado se um recipiente completamente cheio desse líquido for aquecido. No entanto, caso o recipiente sofra uma variação de volume igual à variação volumétrica sofrida pelo líquido, nenhum líquido deverá transbordar.

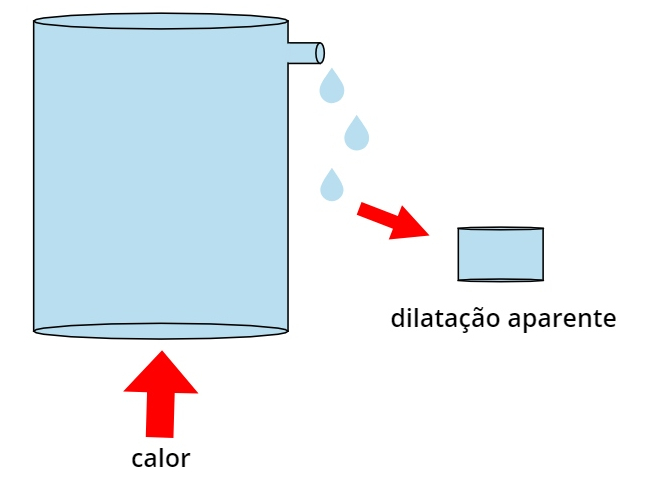
O volume de líquido transbordado na figura corresponde à dilatação aparente.

Fórmulas da dilatação aparente

Para calcularmos o volume de líquido que transborda do frasco, devemos usar a fórmula da dilatação aparente, observe:

ΔV_ap — dilatação aparente (m³)

V₀ — volume inicial do líquido (m³)

γ_ap — coeficiente de dilatação volumétrica aparente (ºC^-1)

ΔT — variação de temperatura (ºC)

Na fórmula anterior, ΔV_ap corresponde ao volume de líquido transbordado, enquanto γ_ap é o coeficiente de dilatação aparente. Para sabermos calcular o coeficiente de dilatação aparente, devemos levar em conta a dilatação sofrida pelo frasco (ΔV_F) que continha o líquido. Para tanto, usaremos a seguinte fórmula:

ΔV_F — dilatação do frasco (m³)

V₀ — volume inicial do frasco (m³)

γ_F — coeficiente de dilatação volumétrica do frasco (ºC^-1)

ΔT — variação de temperatura (ºC)

Na expressão anterior, γ_F refere-se ao coeficiente de dilatação volumétrica do recipiente que contém o líquido, e ΔV_F mede qual foi a dilatação desse frasco. Dessa forma, a dilatação real sofrida pelo líquido (ΔV_R) pode ser calculada como a soma da dilatação aparente com a dilatação do frasco, observe:

ΔV_R — dilatação real do líquido

ΔV_ap — dilatação aparente do líquido

ΔV_R — dilatação real do frasco

Após algumas manipulações algébricas com as fórmulas apresentadas, é possível chegarmos ao seguinte resultado:

γ — coeficiente de dilatação real do líquido (ºC^-1)

γ_F — coeficiente de dilatação volumétrica do frasco (ºC^-1)

γ_ap — coeficiente de dilatação volumétrica aparente (ºC^-1)

A relação acima indica que o coeficiente de dilatação real do líquido pode ser encontrado por meio da soma entre os coeficientes de dilatação aparente e o coeficiente de dilatação do frasco.

Dilatação anômala da água

A água apresenta um comportamento anômalo quanto à dilatação térmica entre as temperaturas de 0 ºC e 4 ºC, entenda: aquecendo-se a água de 0º C para 4ºC, o seu volume diminui, em vez de aumentar. Por essa razão, no estado líquido, a densidade da água tem o seu maior valor para a temperatura de 4ºC. Os gráficos abaixo ajudam a entender o comportamento da densidade e do volume da água em função de sua temperatura, observe:

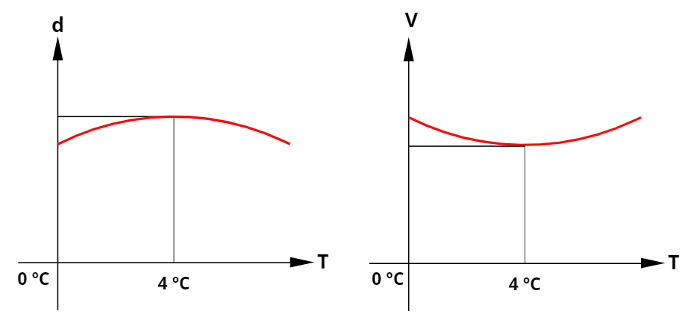
Na temperatura de 4ºC, a densidade da água é a mais alta.

Em razão desse comportamento, os refrigerantes ou garrafas com água estouram quando deixados no congelador por muito tempo. Quando a água atinge a temperatura de 4 ºC, o seu volume é minimamente ocupado pela água em estado líquido, se o resfriamento continuar, o volume da água irá aumentar em vez de diminuir. Quando a água atingir 0 ºC, o volume da água terá crescido grandemente, enquanto o seu recipiente terá reduzido suas próprias medidas, ocasionando a sua ruptura.

As garrafas cheias de água que vão ao congelador podem estourar ao atingirem 0ºC.

Outra consequência desse comportamento anômalo da água é o não congelamento do fundo dos rios em regiões muito frias. Quando a temperatura da água aproxima-se de 0 ºC, sua densidade diminui, e, então, a água fria sobe, em razão do empuxo. Ao subir, a água fria congela-se, formando uma camada de gelo sobre os rios. Como o gelo é um bom isolante térmico, o fundo dos rios mantém-se a, aproximadamente, 4 ºC, pois, nessa temperatura, sua densidade é máxima e tende a permanecer no fundo dos rios.

O motivo por trás do comportamento anômalo da água tem origem molecular: entre 0 ºC e 4 ºC, a atração elétrica entre as moléculas de água supera a agitação térmica, em razão da existência das ligações de hidrogênio presentes entre as moléculas de água.

Veja também: Como ocorre a dilatação anômala da água?

Exercícios resolvidos sobre dilatação dos líquidos

1) Determine o coeficiente de dilatação volumétrica de uma porção de 1 m³ de líquido que sofre uma dilatação de 0,05 m³, quando aquecido de 25ºC para 225ºC.

Resolução:

Vamos calcular o coeficiente de dilatação do líquido em questão utilizando a fórmula da dilatação volumétrica:

Aplicando os dados fornecidos pelo enunciado à fórmula anterior, faremos o seguinte cálculo:

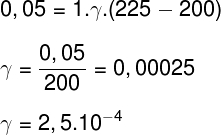
2) Um frasco de vidro, cujo coeficiente de dilatação volumétrica é de 27.10^-6 ºC^-1, apresenta uma capacidade térmica de 1000 ml, à temperatura de 20 ºC, e encontra-se completamente preenchido por um líquido desconhecido. Ao aquecermos o conjunto até 120 ºC, 50 ml de líquido transbordam para fora do recipiente. Determine os coeficientes de dilatação aparente; o coeficiente de dilatação real do líquido; e a dilatação sofrida pelo frasco de vidro.

Resolução:

Vamos calcular o coeficiente de dilatação aparente, para isso, usaremos a fórmula seguinte:

Usando os dados do exercício, faremos o seguinte cálculo:

Em seguida, calcularemos o coeficiente de dilatação real do líquido. Para tanto, precisamos calcular qual foi a dilatação sofrida pelo frasco de vidro:

Substituindo os dados fornecidos pelo enunciado do exercício, temos que resolver o seguinte cálculo:

Com o cálculo acima, determinamos qual foi a dilatação sofrida pelo frasco de vidro. Dessa forma, para encontrarmos a dilatação real do líquido, basta somarmos o volume da dilatação aparente com o volume da dilatação do frasco:

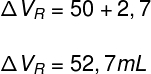
O resultado obtido na resposta acima indica que o líquido no interior do frasco sofreu uma dilatação real de 52,7 mL. Por fim, vamos calcular o coeficiente de dilatação real do líquido:

Usando a fórmula anterior, calculamos o coeficiente de dilatação real da água igual a:

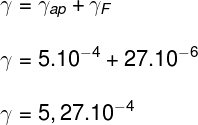
Portanto, o coeficiente de dilatação térmica desse líquido é de 5,27.10^-4 ºC^-1.