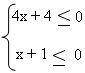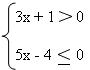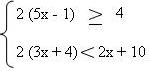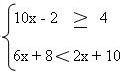PUBLICIDADE
Um sistema de inequação do 1º grau é formado por duas ou mais inequações, cada uma delas tem apenas uma variável sendo que essa deve ser a mesma em todas as outras inequações envolvidas.
Quando terminamos a resolução de um sistema de inequações chegamos a um conjunto solução, esse é composto por possíveis valores que x deverá assumir para que exista o sistema.
Para chegamos a esse conjunto solução devemos achar o conjunto solução de cada inequação envolvida no sistema, a partir daí fazermos a intersecção dessas soluções.
O conjunto formado pela intesecção chamamos de CONJUNTO SOLUÇÃO do sistema.
Veja alguns exemplos de sistema de inequação do 1º grau:
Vamos achar a solução de cada inequação.
4x + 4 ≤ 0
4x ≤ - 4
x ≤ - 4 : 4
x ≤ - 1
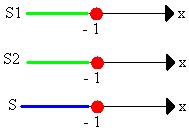
S1 = {x ![]() R | x ≤ - 1}
R | x ≤ - 1}
Fazendo o cálculo da segunda inequação temos:
x + 1 ≤ 0
x ≤ - 1
A “bolinha” é fechada, pois o sinal da inequação é igual.
S2 = { x ![]() R | x ≤ - 1}
R | x ≤ - 1}
Calculando agora o CONJUTO SOLUÇÃO da inequação temos:
S = S1 ∩ S2
Portanto:
S = { x ![]() R | x ≤ - 1} ou S = ] - ∞ ; -1]
R | x ≤ - 1} ou S = ] - ∞ ; -1]
Em primeiro lugar devemos calcular o conjunto solução de cada inequação.
3x + 1 > 0
3x > -1
x > -1
3
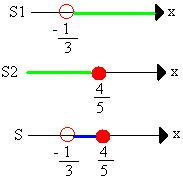
A “bolinha” é aberta, pois o sinal da inequação não é igual.
Calculamos agora o conjunto solução da outra solução.
5x – 4 ≤ 0
5x ≤ 4
x ≤ 4
5
Agora podemos calcular o CONJUNTO SOLUÇÃO da inequação, assim temos:
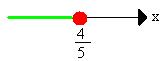
S = S1 ∩ S2
Portanto:
S = { x R | -1 < x ≤ 4} ou S = ] -1 ; 4]
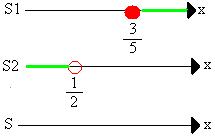
3 5 3 5
Devemos organizar o sistema antes de resolvê-lo, veja como fica:
Calculando o conjunto solução de cada inequação temos:
10x – 2 ≥ 4
10x ≥ 4 + 2
10x ≥ 6
x ≥ 6
10
x ≥ 3
5
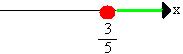
6x + 8 < 2x + 10
6x -2x < 10 – 8
4x < 2
x < 2
4
x < 1
2
Podemos calcular o CONJUNTO SOLUÇÃO da inequação, assim temos:
S = S1 ∩ S2
Observando a solução veremos que não há intersecção, então o conjunto solução desse sistema inequação, será:
S = ![]()
Por Danielle de Miranda
Graduada em Matemática