PUBLICIDADE
A equação do fabricante de lentes é uma fórmula matemática que relaciona a vergência, a distância focal, os índices de refração da lente e do meio em que a lente se encontra, bem como os raios de curvatura das faces interna e externa da lente. Por meio dessa equação, é possível fabricar lentes com diferentes graus, para diferentes finalidades.
Veja também: Óptica — parte da Física que estuda os fenômenos ligados à luz
Tópicos deste artigo
- 1 - Lentes e estudo das lentes
- 2 - Lentes esféricas
- 3 - Equação dos fabricantes de lentes
- 4 - Exercícios resolvidos sobre a equação dos fabricantes de lentes
Lentes e estudo das lentes
O estudo das lentes permite compreender como o material e o formato em que uma lente é feita afetam sua capacidade de mudar a direção de propagação dos raios de luz que a atravessam. Lentes são meios ópticos homogêneos e transparentes que promovem a refração da luz. Quando um feixe de luz passa por uma lente convergente, os raios de luz que o compõem aproximam-se. Quando temos uma lente divergente, os raios de luz afastam-se. Se você não tem muita familiaridade com esses conceitos, sugerimos que você leia o seguinte texto para ter uma base: Principais conceitos da óptica geométrica.
Lentes esféricas
Existem lentes planas e também lentes esféricas. Essas últimas são largamente utilizadas para a correção de problemas visuais, sendo empregadas em óculos e em lentes de contato. Entre as lentes esféricas, ressaltamos a importância de dois tipos de lente: as lentes côncavas e as lentes convexas.
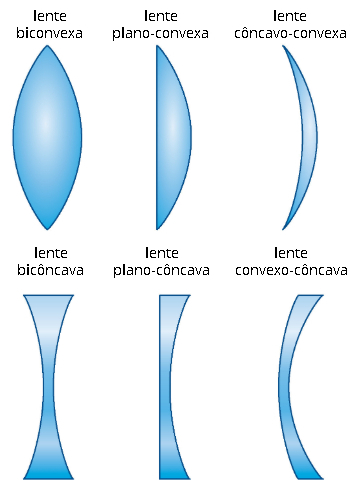
Equação dos fabricantes de lentes
Como ressaltamos, o formato das lentes esféricas afeta a forma como elas direcionam os feixes de luz. A forma exata como a geometria da lente faz isso é descrita pela equação de Halley, também conhecida como a equação dos fabricantes de lentes, uma vez que é por meio dela que as lentes empregadas na correção de problemas visuais são construídas.
A equação do fabricante de lentes é utilizada para calcular o grau, ou vergência, de uma lente esférica. O grau da lente, nesse caso, é chamado dioptria, e sua unidade de medida é o m-¹ ou, simplesmente, di. Portanto, quando nos referimos a uma lente de + 2 graus, essa lente apresenta uma vergência de +2 di.
O sinal que aparece à frente da dioptria indica se a lente é convergente, para o caso de sinal positivo, ou divergente, quando o sinal é negativo. Lentes convergentes fazem com que os raios de luz se cruzem em um ponto mais próximo da lente, enquanto as lentes divergentes distanciam o ponto em que os raios de luz se cruzam, por isso são usadas para corrigir diferentes problemas da visão humana.
A equação dos fabricantes de lentes é a seguinte:
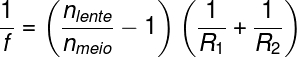
f – distância focal da lente
nlente e nmeio – índices de refração da lente e do meio
R1 e R2 – raios das faces da lente
Os raios de curvatura R1 e R2 são os raios das calotas esféricas que dão origem às lentes esféricas.
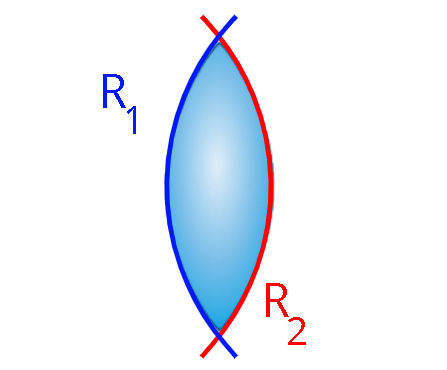
É importante ressaltar que o raio de curvatura das faces planas (quando houver) é infinito. Nesse caso, um dos termos (1/R1 ou 1/R2) torna-se igual a zero. Além disso, n1 e n2 são os índices de refração da lente e do meio em que a lente se encontra imersa, respectivamente.
Veja também: Fenômenos ópticos — eventos extraordinários resultantes da interação da luz com a matéria
Exercícios resolvidos sobre a equação dos fabricantes de lentes
Questão 1 — Determine a vergência de uma lente semiesférica produzida a partir de uma gotícula de glicerina depositada sobre um pequeno orifício de diâmetro igual a 5 mm (logo, o raio dessa lente é de 2,5 mm). Considere o índice de refração da glicerina igual a 1,5.
a) + 200 di
b) – 200 di
c) + 400 di
d) – 400 di
Resolução:
Vamos utilizar a equação dos fabricantes de lentes para resolver essa questão, mas, antes disso, como uma das faces da gota de glicerina é plana, seu raio de curvatura é infinitamente grande, e qualquer número dividido por um número infinitamente grande aproxima-se de zero, dessa maneira, a equação do fabricante de lentes fica um pouco mais simples. Observe:
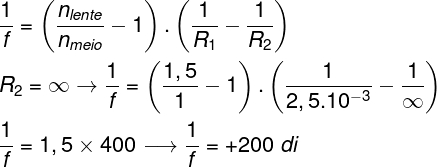
Com base no cálculo, a alternativa correta é a letra A.
Questão 2 — Determine a distância focal da lente descrita na questão anterior e também a ampliação produzida por ela, caso posicionemos um objeto a uma distância de 4 mm dessa lente.
a) + 0,025 m e + 2
b) - 0,005 m e + 5
c) + 0,005 m e + 5
d) – 0,04 m e -4
Resolução:
Para encontrarmos o foco, é preciso utilizar o resultado da vergência, obtido no exercício anterior.
![]()
Para determinarmos a ampliação dessa lente, precisamos fazer o cálculo do aumento linear transversal.
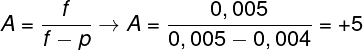
Com base nos resultados, descobrimos que o foco dessa lente é igual a 0,005 m e que o aumento linear dessa lente, para a distância especificada, é igual a + 5, logo a alternativa correta é a letra C.
Por Rafael Helerbrock
Professor de Física






