Lentes esféricas

Lentes esféricas são aparatos ópticos que podem refratar e refletir raios luminosos, formando imagens. Essas lentes são muito utilizadas no cotidiano, já que possibilitam aumentar, diminuir e até mesmo detalhar as imagens ao nosso redor.

Existem dois tipos de lentes esféricas: as lentes convergentes, que convergem os raios, e as lentes divergentes, que espalham os raios. No caso da lente convergente, a formação da imagem depende da posição do objeto frente a ela. Já no caso da lente divergente, obtém-se a mesma imagem, independentemente da posição do observador.

Leia também: Instrumentos ópticos — aqueles que utilizam os fenômenos da luz para produzir imagens

Tópicos deste artigo

• 1 - Resumo sobre as lentes esféricas
• 2 - Quais as propriedades das lentes esféricas?
• 3 - Usos das lentes esféricas
• 4 - Tipos de lentes esféricas
• 5 - Elementos geométricos das lentes esféricas
• 6 - O que são raios notáveis?
• 7 - Como ocorre a formação de imagens nas lentes esféricas?
• 8 - Fórmulas das lentes esféricas
  • Vergência de lentes esféricas
  • Equação dos fabricantes de lentes
• 9 - Vergência de lentes esféricas
• 10 - Justaposição de lentes esféricas

Resumo sobre as lentes esféricas

• Existem diversos usos para as lentes, sendo o principal deles a correção de problemas visuais. Além disso, elas são usadas para ampliação, detalhamento ou diminuição de imagens.

• As lentes esféricas são divididas em dois tipos: convergentes e divergentes.

• Os raios notáveis são os raios luminosos que auxiliam na formação de imagens. Na óptica geométrica, trabalhamos com quatro deles. Porém, para fazermos seus desenhos, são necessários apenas dois.

• A formação das imagens depende do tipo de lente. Através da convexa, são obtidos cinco tipos de imagens. Através da côncava, todas as imagens formadas serão iguais.

• Determina-se a vergência de uma lente por meio do inverso do valor da distância focal, sendo sua unidade de medida a dioptria.

• A justaposição de lentes esféricas é a combinação de diferentes lentes com o objetivo de obter vergências distintas. A justaposição permite reduzir o fenômeno da aberração cromática, por exemplo.

Quais as propriedades das lentes esféricas?

As propriedades das lentes dizem respeito à sua capacidade de convergir raios luminosos nas lentes convexas ou os divergir nas lentes côncavas. Isso pode mudar de acordo com o meio em que essas lentes são inseridas. Normalmente, considera-se que as lentes estão imersas no ar.

Além disso, as lentes esféricas funcionam por meio dos fenômenos de refração e reflexão da luz e, quando incididas em um material homogêneo e transparente, inserido completamente em um meio, são capazes de ampliar ou reduzir o reflexo das imagens.

Usos das lentes esféricas

Lentes esféricas são utilizadas para aumentar ou diminuir as imagens ao nosso redor, por meio do uso, por exemplo, de microscópios e telescópios. Elas são usadas também para correção de problemas visuais, como no caso da lente divergente para solucionar a miopia ou da lente convergente para o problema de hipermetropia.

Leia também: Espelhos planos — superfícies que geram imagens virtuais

Tipos de lentes esféricas

As lentes esféricas são divididas em dois grupos:

• lentes de bordas finas ou lentes divergentes;

• lentes de bordas grossas ou lentes convergentes.

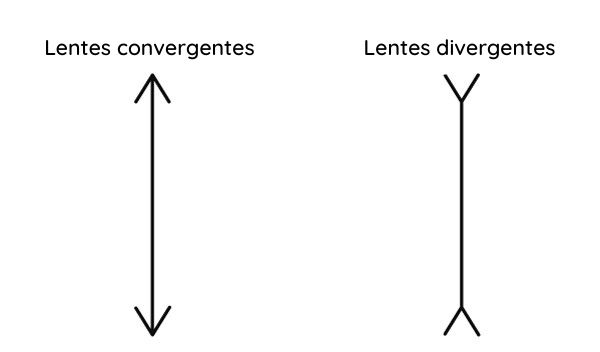
As lentes divergentes são representadas por uma reta com setas viradas para dentro. Já as lentes convergentes são representadas por uma reta com setas viradas para cima, conforme a imagem abaixo:

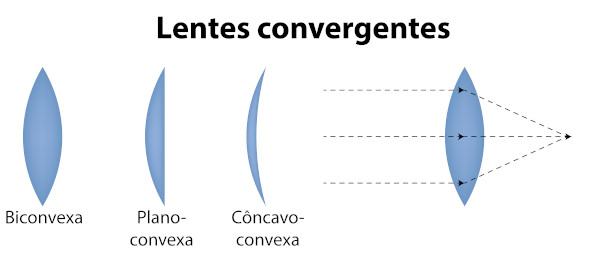
As lentes convergentes podem convergir os raios de luz, ou seja, focar a luz em um ponto específico. Há três tipos delas: as lentes biconvexas, as plano-convexas e as côncavo-convexas.

Já as lentes divergentes podem divergir os raios, ou seja, em vez de os aproximar, elas os espalham. Há três tipos delas: as lentes biconcâvas, as plano-côncavas e as convexo-côncavas.

Elementos geométricos das lentes esféricas

Existem alguns elemetos geométricos comuns a todos os tipos de lentes. São eles:

• Eixo principal (\(E_p\)): linha imaginária que contém os elementos geométricos das lentes.

• Centro óptico (O): é o centro de simetria. Podemos considerar que a sua esquerda é o mundo real, e a sua direita é o mundo virtual, o reflexo.

• Foco principal do objeto (\(f_o\)).

• Foco principal da imagem (\(f_i\)).

• Foco antiprincipal do objeto ou centro de curvatura do objeto (\(A_o\)).

• Foco antiprincipal da imagem ou centro de curvatura da imagem (\(A_i\)).

• Distância focal (f): é a distância entre o centro óptico da lente e o foco principal do objeto.

• Raio de curvatura (R): é a distância entre o centro óptico e o foco antiprincipal do objeto.

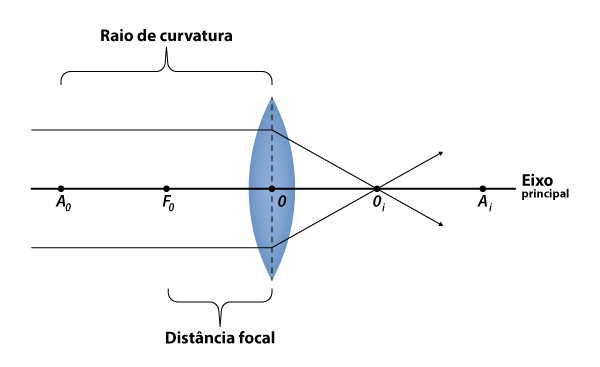
Além dos elementos presentes no eixo principal, há os elementos que usamos para referenciar o objeto e a imagem, sendo eles:

• Posição do objeto (\(p_o\)): posição do objeto no eixo principal.

• Posição da imagem (\(p_i\)): posição da imagem no eixo principal.

• Altura do objeto (o).

• Altura da imagem (i).

O que são raios notáveis?

Os raios notáveis são os feixes provenientes da luz solar refratados pelas lentes esféricas e que formam imagens.

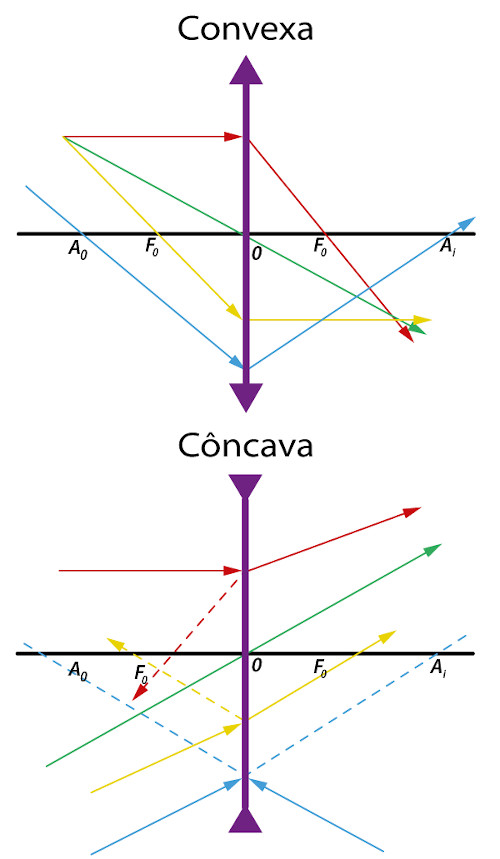
A partir da análise da imagem acima, inferimos que todo raio de luz que:

I - incidir paralelamente ao eixo de simetria será refratado passando pelo foco da imagem (\(f_i\));

II - incidir sobre o foco antiprincipal do objeto (\(A_o\)) será refratado sobre o foco antiprincipal da imagem (\(A_i\)) e vise-versa;

III- incidir sobre o centro óptico será refratado sem sofrer desvio lateral;

IV- incidir no foco do objeto (\({f}_o\)) será refratado paralelamente ao eixo de simetria.

Esses quatro raios notáveis podem funcionar tanto na ida quanto na volta, configurando o princípio da reversibilidade da luz, um dos três princípios da óptica geométrica, sendo os outros dois o princípio da propagação retilínea da luz e o princípio da independência da luz.

Como ocorre a formação de imagens nas lentes esféricas?

A formação de imagens ocorre com o uso de no mínimo dois dos quatro raios notáveis, sendo que no encontro desses raios a imagem é formada.

As imagens podem ser reais ou virtuais. A imagem real é formada do lado direito da lente, sendo invertida e podendo ser projetada. Já a imagem virtual é formada pelo prolongamento dos raios, sendo a imagem direita e impossível de ser projetada.

Além disso, a formação de imagens está sujeita ao tipo de lente. No caso de a lente ser convexa, há cinco configurações diferentes, dependendo da posição do objeto no eixo principal. Porém, se a lente for côncava, a posição do objeto será irrelevante.

• Lente convexa: objeto posicionado antes do foco antiprincipal do objeto \(A_o\). A imagem formada será real, invertida e menor que o objeto.

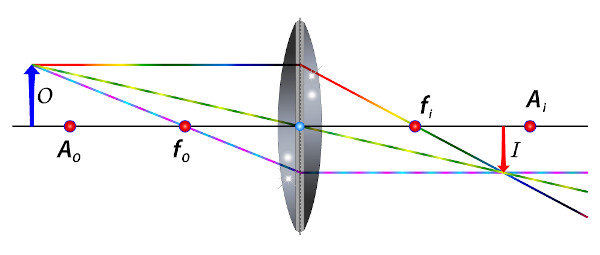
• Lente convexa: objeto posicionado no ponto antiprincipal do objeto \(A_o\). A imagem formada será real, invertida e do mesmo tamanho do objeto.

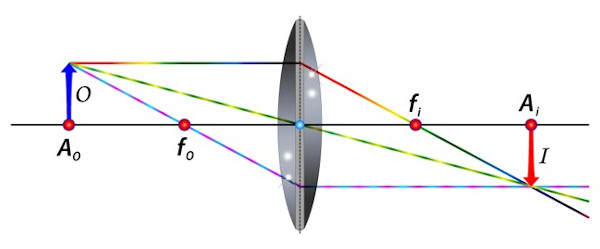
• Lente convexa: objeto posicionado entre o foco do objeto \( f_o\) e o ponto antiprincipal do objeto \(A_o\). A imagem formada será real, invertida e maior que o objeto.

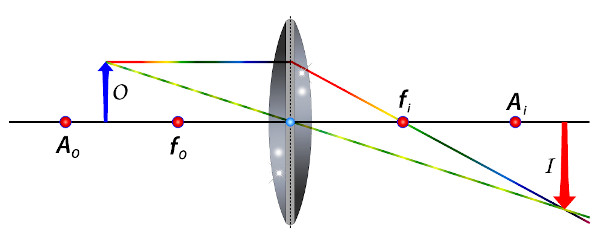
• Lente convexa: objeto posicionado no foco do objeto \(f_o\). Como os raios não se cruzam, não há formação de imagem. Nesse caso, dizemos que a imagem é imprópria. Pode ser que no infinito ela seja formada.

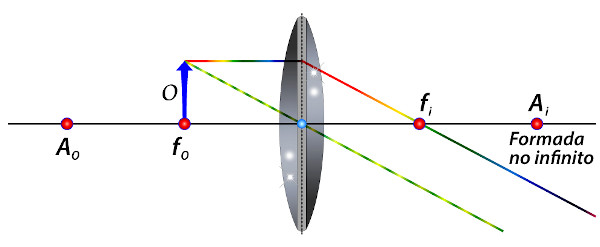
• Lente convexa: objeto posicionado entre o foco do objeto \(f_o\) e o centro óptico O. A imagem formada será virtual, direita e maior que o objeto.

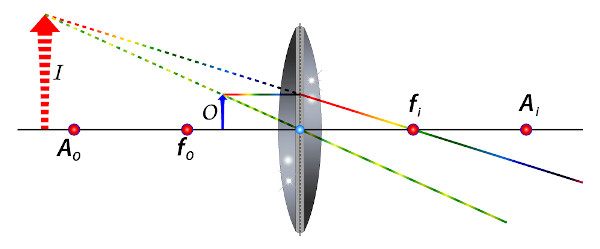
• Lente côncava: todas as imagens serão virtuais, direitas e menores que o objeto.

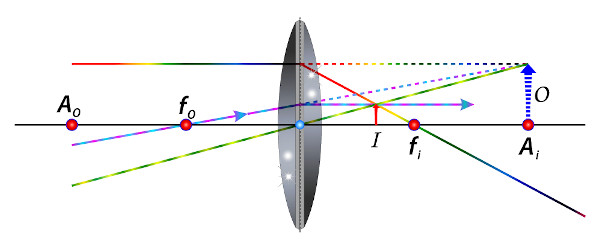
Fórmulas das lentes esféricas

Estão listadas abaixo as fórmulas mais utilizadas nos exercícios de lentes esféricas.

• Vergência de lentes esféricas

\(V=\frac{1}{f}\)

• • \(V\) é a vergência da lente, expressa no inverso do metro, chamada de dioptria (\(m^{-1}\) ou \(di\)).

  • \(f\) é a distância focal, expressa em metros (\(m\)).

• Equação dos pontos conjugados

\(\frac{1}{f}=\frac{1}{p_o}+\frac{1}{p_i}\)

• \(p_o\) é a distância do foco ao objeto, ou posição do objeto.

• \(p_i\) é a distância do foco à imagem, ou posição da imagem.

• Equação do aumento linear transversal

\(A=\frac{i}{o}=\frac{-\ p_i}{p_o}=\frac{f}{f-p_o}\)

• \(A\) é o aumento linear transversal.

• Equação dos fabricantes de lentes

\(V=\frac{1}{f}=\left(\frac{n_{lente}}{n_{meio}}-1\right)=\left(\frac{1}{R_1}+\frac{1}{R_2}\right)\)

• \(n_{lente} \) é o índice de refração do material da lente.

• \(n_{meio}\) é o índice de refração do meio em que a lente está imersa.

• \(R_1\) é o raio de curvatura da face externa da lente.

• \(R_2\) é o raio de curvatura da face interna da lente.

Leia também: Diferenças entre meios transparentes, opacos e translúcidos

Vergência de lentes esféricas

A vergência de uma lente é definida como o inverso da abcissa focal, ou seja, a distância focal dessa lente. Calculamos a vergência através da fórmula:

\(V=\frac{1}{f}\)

Observação: A unidade da vergência é a dioptria, chamada vulgarmente de grau da lente.

De acordo com a convenção de sinais adotada para lentes esféricas delgadas, temos:

• Lentes convergentes: \(f>0\) e \( V>0\)

• Lentes divergentes: \( f<0\) e \(V<0\)

Justaposição de lentes esféricas

A justaposição de lentes esféricas consiste em associar diferentes tipos de lentes a fim de obter configurações de vergência distintas. O cálculo da vergência total é a soma das vergências individuais de cada lente.

Essa prática é adotada no intuito de reduzir o fenômeno da aberração cromática que ocorre quando raios luminosos com diferentes comprimentos de onda atravessam diferentes pontos focais ou para aumentar o efeito produzido por uma lente.

Por Pâmella Raphaella Melo
Professora de Física