O estudo analítico da reta é muito utilizado em problemas cotidianos ligados a diversas áreas do conhecimento, como a física, biologia, química, engenharia e até a medicina. Determinar a equação da reta e compreender seus coeficientes é bastante importante para a compreensão do seu comportamento, sendo possível analisar sua inclinação e os pontos onde intercepta os eixos do plano. Sobre as retas temos os seguintes tipos de equação: equação geral da reta, equação reduzida, equação paramétrica e equação segmentária. Faremos o estudo da equação segmentária da reta e sua utilização.
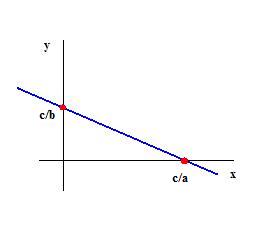
Considere uma reta s qualquer do plano de equação ax + by = c. Para obtenção da equação segmentária da reta s basta dividir toda a equação por c, obtendo:
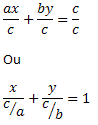
Que é a equação na forma segmentária da reta s.
c/a é a abscissa do ponto de interseção com o eixo x.
c/b é a ordenada do ponto de interseção com o eixo y
Exemplo 1. Determine a forma segmentária da equação da reta s cuja equação geral é:
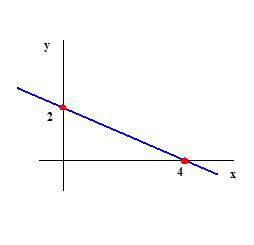
s: 2x + 3y – 6 = 0
Solução: Para determinar a equação segmentária da reta s devemos isolar o termo independente c. Assim, segue que:
2x + 3y = 6
Dividindo a equação por 6, obtemos:
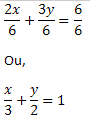
A identidade acima é a forma segmentária da equação da reta s.
Exemplo 2. Determine a equação segmentária da reta t: 7x + 14y – 28 =0 e as coordenadas dos pontos de interseção da reta com os eixos do plano.
Solução: Para determinar a forma segmentária da equação da reta t devemos isolar o termo independente c. Assim, teremos:
7x + 14y = 28
Dividindo toda igualdade por 28, obtemos:
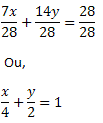
Que é a equação segmentária da reta t.
Com a equação segmentária, podemos determinar os pontos de interseção da reta com os eixos ordenados do plano. O termo que divide x na equação segmentária é abscissa do ponto de intercessão da reta com o eixo x, e o termo que divide y é abscissa do ponto de interseção da reta com o eixo y. Assim:
(4, 0) é o ponto de interseção da reta com o eixo x.
(0, 2) é o ponto de interseção da reta com o eixo y.
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola