Soma dos Termos de uma PG Infinita

A soma dos termos de uma progressão geométrica finita é dada pela expressão:

  , onde q (razão) é diferente de 1. Alguns casos em que a razão q pertence ao intervalo –1 < q < 1, verificamos que quando o número de elementos n se aproxima do infinito (+∞), a expressão qⁿ tende ao valor zero. Portanto, substituindo qⁿ por zero na expressão da soma dos termos de uma PG finita teremos uma expressão capaz de determinar a soma dos termos de uma PG infinita dentro do intervalo –1 < q < 1, observe:

Exemplo 1

Determine a soma dos elementos da seguinte PG:  .

 


Exemplo 2

A expressão matemática da soma dos termos de uma PG infinita é recomendada na obtenção da fração geratriz de uma dízima periódica simples ou composta. Observe a demonstração.
Considerando a dízima periódica simples 0,222222 ..., vamos determinar sua fração geratriz.

Exemplo 3

Vamos determinar a fração que origina o seguinte número decimal 0,231313..., classificado como uma dízima periódica composta.

Exemplo 4

Determine a soma dos elementos da progressão geométrica dada por (0,3; 0,03; 0,003; 0,0003; ...).

Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola

Progressões - Matemática - Brasil Escola
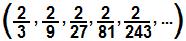