PUBLICIDADE
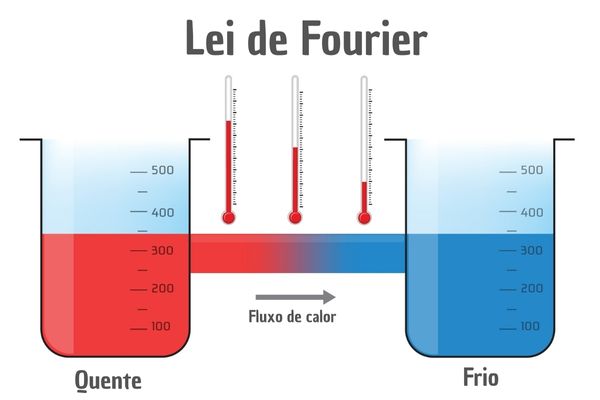
A lei de Fourier é uma lei da Termologia desenvolvida pelo cientista Jean Fourier a respeito do fluxo de calor entre corpos e paredes, o qual se altera de forma proporcional à condutividade térmica do material, à área da secção transversal e à variação de temperatura entre as extremidades e se altera de forma inversamente proporcional à espessura.
Saiba mais: Primeira lei da termodinâmica — uma aplicação do princípio da conservação da energia
Tópicos deste artigo
- 1 - Resumo sobre lei de Fourier
- 2 - O que é a lei de Fourier?
- 3 - Fórmulas da lei de Fourier
- 4 - Unidades de medida da lei de Fourier
- 5 - Como calcular a lei de Fourier?
- 6 - Lei de Fourier no Enem
- 7 - Exercícios resolvidos sobre lei de Fourier
Resumo sobre lei de Fourier
-
A lei de Fourier afirma que o fluxo de calor em um corpo varia de forma proporcional à variação de temperatura.
-
Ela é calculada pelo produto entre a condutividade térmica, a área da secção transversal e a variação de temperatura, todas divididas pela espessura da parede.
-
O fluxo de calor é inversamente proporcional à espessura da parede.
-
A unidade de medida do fluxo de calor é o Watt.
-
A lei de Fourier é um conteúdo que pode ser cobrado de diversas formas no Enem, com exemplos práticos, teoria e até cálculos usando sua fórmula.
O que é a lei de Fourier?
A lei de Fourier, também conhecida como lei da condução térmica, trata do fluxo de calor em corpos homogêneos que estão em um regime estacionário de condução, que é proporcional à condutividade térmica do material, à área da secção transversal e à variação de temperatura, mas é inversamente proporcional à espessura.
Ela foi formulada pelo físico e matemático Jean Baptiste Joseph Fourier (1768-1830), conhecido por barão de Fourier, que estudava experimentalmente a propagação de calor por condução.
Fórmulas da lei de Fourier
→ Lei de Fourier
\(\Phi=\frac{k\cdot A\cdot∆T}{l}\)
-
Φ → fluxo de calor, medido em Watt \([W]\).
-
k → condutividade térmica, medida em \([W/m\cdot K]\).
-
A → área da secção transversal, medida em \( [m^2]\).
-
∆T → variação de temperatura entre as regiões separadas pela parede, medida em Kelvin \([K]\).
-
l → espessura da parede ou extenssão atravessada, medida em metros \([m]\).
→ Fluxo de calor
\(\Phi=\frac{Q}{∆t}\)
-
Φ → fluxo de calor, medido em Watt \([W]\).
-
Q → quantidade de calor, medida em Joule \([J]\).
-
∆t → variação do tempo de transmissão, medida em segundos \( [s]\).
→ Calor relacionado à lei de Fourier
\(Q=\frac{k\cdot A\cdot∆T\cdot∆t}{l}\)
-
Q → quantidade de calor, medida em Joule \([J]\).
-
k → condutividade térmica, medida em \([W/m\cdot K]\).
-
A → área da secção transversal, medida em \( [m^2]\).
-
∆T → variação de temperatura entre as regiões separadas pela parede, medida em Kelvin \([K]\).
-
∆t → variação do tempo de transmissão, medida em segundos \([s]\).
-
l → espessura da parede ou extenssão atravessada, medida em metros \([m]\).
Unidades de medida da lei de Fourier
Diversas unidades de medida são empregadas na lei de Fourier. A seguir, veremos uma tabela com as unidades de medida de acordo com o Sistema Internacional de Unidades (S.I.), outra forma comum em que elas aparecem e como converter uma na outra.
|
Grandezas físicas |
Unidades de medida de acordo com o S.I. |
Unidades de medida em outro formato |
Conversão das unidades de medida |
|
Fluxo de calor |
W ou \(\frac{J}{s}\) |
\(\frac{cal}{s}\) |
Feita por meio da conversão das unidades de medida das outras grandezas físicas. |
|
Quantidade de calor |
Joule |
Caloria |
\(1\ cal=4,2\ J\) |
|
Condutividade térmica |
\(W/m\cdot K\) ou \(\frac{J\cdot m}{s\cdot m^2\cdot K}\) |
\(\frac{cal}{s\cdot cm\cdot °C}\) |
Feita por meio da conversão das unidades de medida das outras grandezas físicas. |
|
Área da secção transversal |
Metros quadrados |
Centímetros quadrados |
\(1\ cm^2=0,0001\ m^2\) |
|
Temperatura |
Kelvin |
Celsius |
\(°C=K-273\) |
|
Tempo |
Segundos |
Minutos |
1 min = 60 s |
|
Espessura |
Metros |
Centímetros |
1 cm = 0,01 m |
Como calcular a lei de Fourier?
A lei de Fourier é usada sempre que trabalhamos com propagações de calor por condução térmica, aquelas em que o aquecimento ocorre de átomo em átomo, mas também pode ser utilizada para calcular o fluxo de calor entre diferentes corpos, como veremos no exemplo a seguir.
-
Exemplo:
Duas salas vizinhas possuem temperaturas de \(T_2=40 °C\) e \(T_1=20 °C\) e estão separadas por uma parede fina de 0,2 cm de espessura, com área de 20 000 cm². Sabendo que a condutividade térmica dessa parede é de \(0,082\ cal/s\cdot cm\cdot °C\), qual foi o fluxo de calor entre elas?
Resolução:
Encontraremos o fluxo de calor usando a fórmula da lei de Fourier:
\(\Phi=\frac{k\cdot A\cdot∆T}{l}\)
\(\Phi=\frac{k\cdot A\cdot(T_f-T_i)}{l}\)
Nesse caso, não há necessidade de converter as unidades de medida, porque todas são proporcionais:
\(\Phi=\frac{0,082\cdot20\ 000\cdot(40-20)}{0,2}\)
\(\Phi=\frac{0,082\cdot20\ 000\cdot(20)}{0,2}\)
\(\Phi=\frac{32\ 800}{0,2}\)
\(\Phi=164\ 000\)
\(\Phi=164\ \frac{kcal}{s}\)
O fluxo de calor foi de 164 kcal por segundo.
Leia também: Quais são os processos de propagação de calor?
Lei de Fourier no Enem
A lei de Fourier pode ser cobrada de maneira teórica ou prática no Enem. No contexto teórico, podemos encontrar questões envolvendo seus conceitos e/ou cálculos. Já na prática, podem ser utilizadas situações do cotidiano, como o calor e temperatura, ou situações envovendo experimentos em que teremos que analisar se e como ocorre a transmissão de calor, por exemplo. Vale lembrar que o Enem costuma cobrar a Física do cotidiano, mas é fundamental compreender a teoria e as fórmulas.
Exercícios resolvidos sobre lei de Fourier
Questão 1
(IME — adaptada) Um vidro plano, com coeficiente de condutibilidade térmica \(0,00183\ cal/s\cdot cm\cdot °C\), tem uma área de 1000 cm² e espessura de 3,66 mm. Sendo o fluxo de calor por condução através do vidro de 2000 calorias por segundo, calcule a diferença de temperatura entre suas faces.
A) 0,4 °C
B) 400 °C
C) 4000 °C
D) 40 °C
E) 4 °C
Resolução:
Alternativa B
Primeiramente, vamos conveter a espessura de milímetros para centímetros:
\(3,66\ mm=0,366\ cm\)
Encontraremos o fluxo de calor por meio da fórmula da lei de Fourier:
\(\Phi=\frac{k\cdot A\cdot∆T}{l}\)
\(2000=\frac{0,00183\cdot 1000\cdot∆T}{0,366}\)
\(2000=\frac{1,83\cdot∆T}{0,366}\)
\(2000=5\cdot∆T\)
\(∆T=20005\)
\(∆T=400 °C\)
Questão 2
(UFT) Uma sala de estúdio é mantida à temperatura de 20 °C e encontra-se separada de uma sala vizinha, à temperatura ambiente de 30 °C, por uma janela retangular de vidro de 8,0 mm de espessura, 1,0 m de altura por 1,5 m de largura. Sabendo que a condutividade térmica do vidro é de \(0,80\ W/m\cdot K\), o total de calorias transmitidas pela janela após 4,2 minutos é de, aproximadamente:
A) 1,50 kcal.
B) 37,8 kcal.
C) 60,0 kcal.
D) 90,0 kcal.
E) 126 kcal.
Resolução:
Alternativa D
De início, converteremos o tempo de minutos em segundos:
\(4,2\ min=252\ s\)
Devemos também converter a espessura de milímetros em metros:
\(8,0\ mm=0,008\ m\)
Então, para calcular o calor transmitido, usaremos a fórmula do calor relacionado à lei de Fourier:
\(Q=\frac{k\cdot A\cdot∆T\cdot∆t}{l}\)
\(Q=\frac{k\cdot A\cdot(T_F-T_I)\cdot∆t}{l}\)
\(Q=\frac{0,8\cdot1,5\cdot(30-20)\cdot252}{0,008\ }\)
\(Q=\frac{0,8\cdot1,5\cdot(10)\cdot252}{0,008\ }\)
\(Q=378\ 000\ J\)
Lembrando que 1 cal = 4,2 J, então o calor em Joule é:
\(Q=\frac{378\ 000\ J}{4,2}=90\ 000\ cal=90\ kcal\)
Por Pâmella Raphaella Melo
Professora de Física
