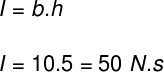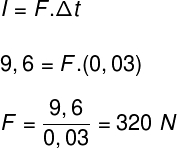O impulso é uma grandeza física vetorial definida pelo produto da força média aplicada sobre um corpo pelo intervalo de tempo. O impulso também pode ser definido a partir da variação da quantidade de movimento sofrida por um corpo.
Tópicos deste artigo
- 1 - Resumo sobre Impulso
- 2 - O que é impulso na Física?
- 3 - Usos cotidianos do impulso
- 4 - Impulso e quantidade de movimento
- 5 - Teorema do impulso
- 6 - Fórmula do impulso
- 7 - Gráfico para cálculo do impulso de uma força variável
- 8 - Exemplos de gráficos de impulso
- 9 - Exercícios de impulso
Resumo sobre Impulso
-
Impulso é uma grandeza física vetorial. Sua unidade é N.s (Newton vezes segundo) ou kg.m/s (quilograma vezes metro por segundo).
Anuncie aqui -
O impulso pode ser calculado por meio do produto da força média aplicada sobre um corpo pelo intervalo de tempo de aplicação dessa força.
-
O impulso também pode ser entendido como a mudança da quantidade de movimento de um corpo, por isso, podemos defini-lo como a diferença entre as quantidades de movimento final e inicial de um corpo.
-
O teorema do impulso diz que a aplicação de uma força sobre um corpo durante um determinado intervalo de tempo resulta em uma variação da sua quantidade de movimento.
O que é impulso na Física?
Impulso é uma grandeza física que mede a mudança da quantidade de movimento sofrida por um corpo sobre o qual atua uma força (F) durante um intervalo de tempo (Δt). O impulso é uma grandeza vetorial, isto é, apresenta módulo, direção e sentido, e sua unidade no sistema internacional de unidades (SI) é o kg.m/s ou, simplesmente, N.s.
O principal uso do impulso na Física é voltado para o estudo das colisões entre os corpos. Durante as colisões, é comum que as forças mútuas exercidas entre os corpos sejam variáveis, fazendo-se necessário o uso do impulso para o cálculo das velocidades ou das quantidades de movimento dos corpos envolvidos nas colisões. A ideia é simples: se pudermos medir o intervalo de tempo de uma colisão, seremos capazes de determinar o valor médio da força exercida sobre os corpos.
Veja também: A física das colisões
A fórmula utilizada para o cálculo do impulso na Física é mostrada na figura abaixo:
![]()
Legenda:
I – impulso (kg.m/s ou N.s)
Fm – força média (N)
Δt – intervalo de tempo (s)
A fórmula mostrada acima indica que o impulso sofrido por um corpo é proporcional à força exercida sobre ele e ao intervalo de tempo de aplicação dessa força. Portanto, quanto maior for o impulso, maiores serão a força aplicada sobre o corpo e a duração da aplicação dessa força.
Veja também: O que são grandezas diretamente e inversamente proporcionais
O impulso também equivale à mudança da quantidade de movimento de um corpo. Quando aplicamos uma força em um corpo durante certo intervalo de tempo, a velocidade do corpo pode sofrer variações, por isso, o impulso também pode ser definido em relação à mudança da quantidade de movimento de um corpo. Observe:
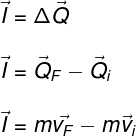
Legenda:
I – Impulso (N.s ou kg.m/s)
ΔQ – variação da quantidade de movimento (N.s ou kg.m/s)
QF – quantidade de movimento final (N.s ou kg.m/s)
Qi – quantidade de movimento inicial (N.s ou kg.m/s)
m – massa (kg)
vF – velocidade final (m/s)
vi – velocidade inicial (m/s)
Por fim, podemos dizer que o produto da força pelo intervalo de tempo de aplicação dessa força equivale à variação da quantidade de movimento:
A relação estabelecida na equação acima é conhecida como teorema do impulso.
Usos cotidianos do impulso
Pode parecer que não, mas o impulso é utilizado cotidianamente para diminuir o módulo da força exercida sobre um corpo durante as colisões. Confira alguns exemplos práticos de aplicação do conceito de impulso:
-
Atualmente, os para-choques presentes nos veículos são feitos de materiais elásticos. Durante uma batida, esses para-choques sofrem grandes deformações até o veículo parar completamente. Isso aumenta o tempo da batida, diminuindo, assim, o módulo da força média exercida sobre o automóvel. Dessa forma, os passageiros no interior do veículo sofrerão menos com a desaceleração.
-
Quando um boxeador prepara-se para receber um golpe do qual não conseguiu desviar-se, ele desloca seu rosto para trás, aumentando o tempo de contato do golpe, diminuindo, assim, a força exercida sobre ele.
-
Ao pularmos de qualquer altura, é comum cairmos com as pernas esticadas e dobrarmos os joelhos até chegarmos no chão. Isso faz com que o tempo de contato com o solo aumente e a força média exercida na queda diminua.
Anuncie aqui
Veja também: A relação entre impulso e uso de airbags
Em resumo, a força média exercida durante uma colisão é inversamente proporcional à sua duração:
Logo, o tempo de uma colisão e a força exercida sobre o corpo são grandezas inversamente proporcionais.
Impulso e quantidade de movimento
A unidade do impulso é a mesma utilizada na quantidade de movimento: kg.m/s. Além disso, dizemos que o impulso que é aplicado sobre um corpo é igual à variação da quantidade de movimento desse corpo:
.jpg)
Legenda:
I – impulso (N.s ou kg.m/s)
ΔQ – variação da quantidade de movimento (N.s ou kg.m/s)
QF – quantidade de movimento final (N.s ou kg.m/s)
Qi – quantidade de movimento inicial (N.s ou kg.m/s)
m – massa (kg)
vF – velocidade final (m/s)
vi – velocidade inicial (m/s)
Confira abaixo um exemplo de aplicação do conceito de impulso:
Exemplo 1
Calcule o módulo do impulso exercido pelo motor de um veículo de 800 kg que acelera de uma velocidade inicial de 20 m/s até 30 m/s.
Resolução
O impulso exercido sobre o veículo pode ser determinado por meio da variação da quantidade de movimento, isto é, equivale à quantidade de movimento final subtraída da quantidade de movimento inicial. Logo, o módulo desse impulso é dado por:
O resultado acima nos indica que, sobre esse veículo, agiu uma força média de 8000 N a cada segundo.
Teorema do impulso
O teorema do impulso afirma que o módulo da força aplicada sobre um corpo durante determinado intervalo de tempo resulta em uma variação da quantidade de movimento do corpo. Em termos práticos, fica simples entender: quanto mais tempo passarmos exercendo força sobre um corpo, maior será a variação de velocidade sofrida por esse corpo. A fórmula utilizada para definir o teorema do impulso é apresentada abaixo:
Além disso, é importante lembrarmos que impulso e quantidade de movimento são grandezas vetoriais, isto é, ao realizarmos cálculos que envolvam essas grandezas, devemos fazer somas vetoriais, que levam em conta a direção e o sentido do movimento. Para tanto, é possível adotarmos algumas regras simples:
-
Adote um referencial para a resolução do exercício, por exemplo: nas direções vertical e horizontal, adote os sentidos esquerda-direita e baixo-cima com o sinal positivo. Todos os corpos que se moverem nesse sentido receberão sinais positivos para sua quantidade de movimento, enquanto os demais receberão sinais negativos.
-
Caso um corpo esteja movendo-se em duas direções, como no caso de um corpo que tenha quantidades de movimento na direção horizontal e vertical, devemos aplicar o teorema de Pitágoras em virtude da ortogonalidade desses vetores.
Confira abaixo um exemplo sobre a aplicação do teorema do impulso:
Exemplo 2
Uma força de 120,0 N é aplicada em uma pequena bolinha de tênis de 0,050 kg por uma raquete durante um intervalo de tempo igual a 0,01 s. Sabendo que a bolinha movia-se no sentido direita-esquerda e, imediatamente antes de tocar a raquete, encontrava-se com velocidade de 15 m/s, calcule:
a) O módulo do impulso exercido sobre a bola.
b) A velocidade final da bola.
Resolução
a) Para calcularmos o módulo do impulso exercido sobre a bola, usaremos a fórmula abaixo:
Logo, teremos um impulso igual a:
b) Para calcularmos a velocidade final da bola, usaremos a seguinte definição de impulso:
Devemos ficar atentos ao sentido de movimento da bola: a força exercida sobre ela e sua velocidade final são horizontais no sentido esquerda-direita. Já a velocidade inicial da bola está no sentido direita-esquerda, portanto, deve ter um sinal diferente. Dessa forma, teremos:
Fórmula do impulso
As fórmulas do impulso estão resumidas abaixo:
→ Fórmula do impulso
→ Relação do impulso com a variação da quantidade de movimento
Gráfico para cálculo do impulso de uma força variável
É comum encontrarmos exercícios que envolvam forças variáveis. Nesses casos, podemos determinar o impulso exercido sobre um corpo por meio da área do gráfico da força pelo intervalo de tempo de aplicação dessa força:
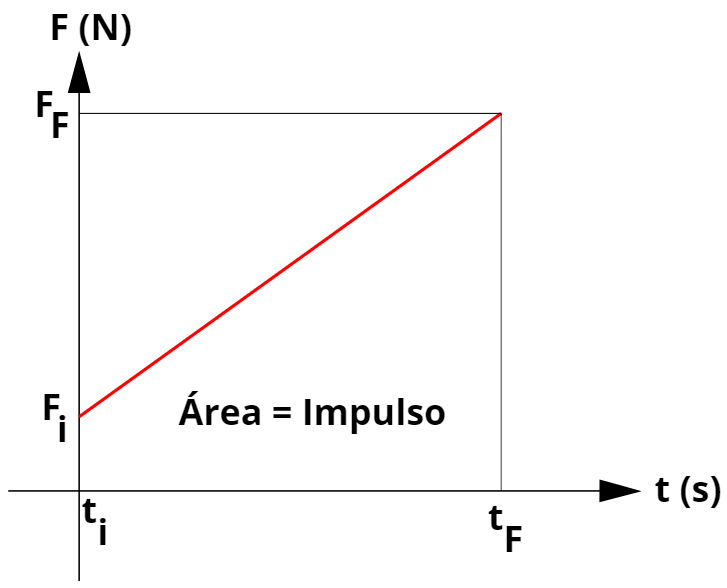
Legenda:
FF – força final (N)
Fi - força inicial (N)
ti – instante inicial (s)
tF – instante final (s)
Para determinarmos o módulo do impulso sofrido pelo corpo, basta calcularmos a área do gráfico.
Veja também: Impulso de força variável
Exemplos de gráficos de impulso
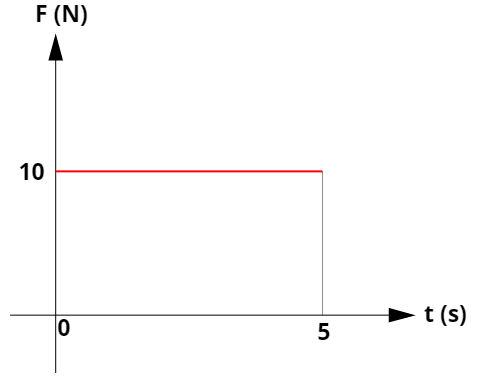
Uma partícula recebe um impulso externo de uma força segundo o gráfico apresentado abaixo:
Considere que, após a aplicação da força, a velocidade da partícula seja mantida na mesma direção e no mesmo sentido. Determine a quantidade de movimento adquirida pelo corpo.
Resolução
Como sabemos, a área do gráfico de força por tempo fornece-nos o impulso exercido sobre o corpo. Dessa forma, temos que:
Como o teorema do impulso informa que o impulso exercido sobre um corpo é igual à sua variação de quantidade de movimento, logo, essa variação é de 50 N.s.
Exercícios de impulso
(FUVEST) Após o chute para a cobrança de uma penalidade máxima, uma bola de futebol de massa igual 0,40 kg sai com velocidade igual a 24 m/s. O tempo de contato entre o pé do jogador e a bola é de 3,0.10-2 s.
a) Qual é a quantidade de movimento adquirida pela bola com o chute?
b) Qual é a força média aplicada pelo pé do jogador sobre a bola?
Resolução
a) Vamos calcular a quantidade de movimento que foi adquirida pela bola. Para tanto, consideramos que, durante a cobrança de pênalti, a bola encontrava-se em repouso. Portanto, o impulso adquirido por ela pode ser calculado da seguinte forma:
b) Para calcular a força média aplicada durante o chute, utilizaremos a equação a seguir:
Por Me. Rafael Helerbrock

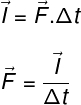


.jpg)

.jpg)