As funções horárias do MUV são equações utilizadas para descrever a trajetória de corpos que se movem com aceleração constante. Elas possibilitam parâmetros para determinar posição, velocidade ou aceleração em um determinado instante de tempo, sendo, portanto, equações de fundamental importância para o estudo do movimento no âmbito da cinemática.
Veja também: 10 equações de Física essenciais para o Enem
Tópicos deste artigo
Quais são as funções horários do MUV?
O movimento uniformemente variado é aquele em que um corpo sofre uma aceleração constante, de modo que sua velocidade varia de forma igual a cada segundo. O estudo do MUV requer que saibamos utilizar as funções horárias da velocidade e da posição, que são, respectivamente, funções do 1º grau e do 2º grau.

As funções horárias do MUV são equações que dependem do tempo como variável.
Quando um móvel que descreve um MUV sofre uma variação positiva de velocidade, dizemos que seu movimento é acelerado. Por outro lado, se essa variação é negativa, dizemos que o movimento é desacelerado ou retardado.
A aceleração é um dos conceitos centrais do MUV. Essa grandeza pode ser calculada pela variação da velocidade dividida por um intervalo de tempo. No Sistema Internacional de Unidades, a unidade de medida da aceleração é o m/s², que significa a mudança na velocidade, em m/s, a cada segundo.
→ Função horária da velocidade no MUV
A função horária da velocidade do MUV é uma equação em que a velocidade do móvel é escrita em função do instante de tempo. Essa função é uma equação de 1º grau, ou seja, é a equação de uma reta.
![]()
v(t) – velocidade no instante t (m/s)
v0 – velocidade inicial (m/s)
a – aceleração (m/s²)
t – instante de tempo (s)
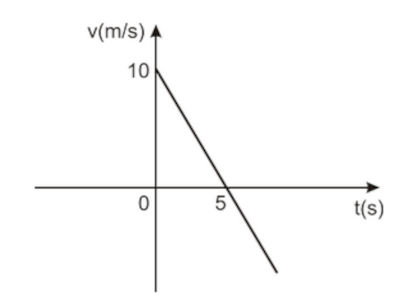
A figura a seguir apresenta o gráfico da função horária da posição, que relaciona a velocidade com o tempo.
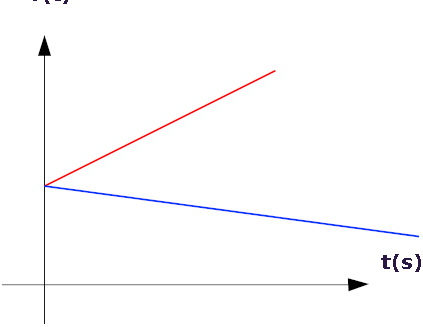
Na figura acima, as retas vermelha e azul representam, respectivamente, um movimento acelerado e um movimento retardado. O ponto em que essas retas tocam o eixo vertical é a velocidade inicial do movimento. Além disso, quanto maior é a inclinação dessas retas em relação ao eixo horizontal, maior é o módulo da velocidade.
→ Função horária da posição no MUV
A função horária da posição é a equação usada para determinar a posição de um móvel que descreve um movimento uniformemente variado. Trata-se de uma equação do 2º grau que depende de variáveis como velocidade inicial, posição inicial e aceleração.
A função horária da posição é a seguinte:
![]()
S(t) – posição no instante t (m)
S0 – posição inicial (m)
Na figura a seguir, exibimos um gráfico qualitativo que relaciona a posição de um corpo que descreve um MUV com relação ao tempo.
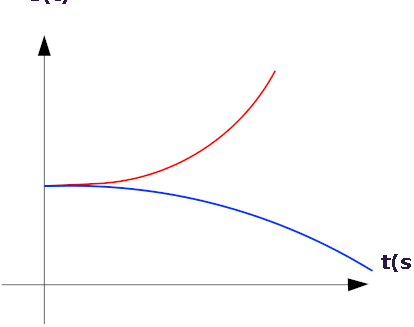
O gráfico acima mostra duas curvas, uma vermelha e uma azul, que representam, respectivamente, os movimentos acelerado e retardado. Perceba que a concavidade da parábola é o que define se o movimento é acelerado ou não: quando a concavidade está virada para cima, a aceleração é positiva. No gráfico, a posição inicial de ambos os movimentos se encontra no ponto onde as curvas cruzam o eixo vertical.
Veja também: Principais conceitos e fórmulas do movimento retilíneo uniforme
Exercícios resolvidos sobre as funções horárias do MUV
Questão 1 — (UTF-PR) Um ciclista movimenta-se em sua bicicleta, partindo do repouso e mantendo uma aceleração aproximadamente constante de valor médio igual a 2,0 m/s². Depois de 7,0 s de movimento, atinge uma velocidade, em m/s, igual a:
a) 49
b) 14
c) 98
d) 35
e) 10
Resolução:
Vamos resolver a questão e, para isso, utilizaremos os dados informados pelo exercício, bem como a função horária da posição.
![]()
Com base no cálculo, descobrimos que a velocidade final do móvel é de 14 m/s, portanto a alternativa correta é a letra B.
Questão 2 — (UFPR) Um motorista conduz seu automóvel pela BR-277 a uma velocidade de 108 km/h quando avista uma barreira na estrada, sendo obrigado a frear (desaceleração de 5 m/s²) e parar o veículo após certo tempo. Pode-se afirmar que o tempo e a distância de frenagem serão, respectivamente:
a) 6 s e 90 m.
b) 10 s e 120 m.
c) 6 s e 80 m.
d) 10 s e 200 m.
e) 6 s e 120 m.
Resolução:
Primeiramente vamos determinar qual é o tempo de frenagem. Observe o cálculo a seguir, pois fazemos uso da função horária da velocidade:
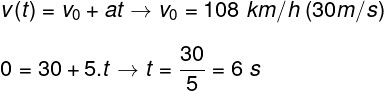
Para fazermos o cálculo acima, foi necessário transformar a unidade da velocidade, que estava em km/h, em m/s, dividindo-a pelo fator 3,6. O próximo cálculo diz respeito ao deslocamento do carro até a parada completa. Para fazê-lo, vamos usar a função horária da posição:
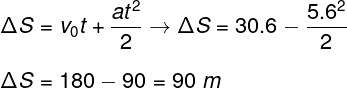
Com base no cálculo, descobrimos que o deslocamento do veículo, desde o início da frenagem até a parada completa, é de 90 m. Com base nisso e no cálculo anterior, a alternativa correta é a letra A.
Por Rafael Helerbrock
Professor de Física