Aceleração Escalar

Aceleração escalar média é uma grandeza física que mede a variação da velocidade (Δv) de um móvel em um determinado intervalo de tempo (Δt). A unidade de aceleração no Sistema Internacional de unidades é o m/s².

Veja também: Introdução ao estudo da Cinemática

A palavra escalar denota que essa grandeza, a aceleração escalar média, é completamente definida pelo seu módulo, não sendo necessário especificar uma direção e um sentido para ela. Isso é possível, uma vez que a maior parte dos exercícios sobre esse assunto envolve movimentos unidimensionais. A palavra média, por sua vez, indica que a aceleração calculada representa uma média e não é, necessariamente, igual à aceleração a cada instante de um movimento.

Para calcularmos a aceleração escalar média de um móvel, utilizamos a seguinte equação:

a – aceleração média (m/s²)
Δv – variação de velocidade (m/s)
Δt – intervalo de tempo (s)

Na equação acima, Δv diz respeito à mudança no módulo da velocidade. Podemos calcular essa variação de velocidade usando a seguinte igualdade: Δv = v_F – v₀. O intervalo de tempo Δt é calculado de maneira similar: Δt = t_F – t₀. Por isso, é possível reescrever a fórmula de aceleração média mostrada acima de forma mais completa:

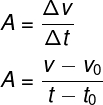
v – velocidade final
v₀ – velocidade final
t – instante final
t₀ – instante inicial

Tópicos deste artigo

• 1 - Função horária da velocidade
• 2 - Gráficos do movimento acelerado
• 3 - Aceleração escalar constante
• 4 - Cálculo do deslocamento com aceleração constante
• 5 - Aceleração escalar instantânea
• 6 - Exercícios de aceleração escalar média

Função horária da velocidade

Quando um móvel acelera de forma constante, isto é, quando a sua velocidade muda de forma igual para intervalos de tempos iguais, podemos determinar a sua velocidade final (v) após um intervalo de tempo de aceleração constante (a) usando a sua função horária da velocidade, confira:

Veja também: Grandezas vetoriais e escalares

Gráficos do movimento acelerado

A equação acima mostra que a velocidade final de um móvel é dada por sua velocidade inicial acrescida do produto de sua aceleração pelo tempo. Perceba que a função mostrada na fórmula anterior é uma função de 1º grau, similar a uma equação da reta. Por isso, os gráficos de posição e velocidade em função do tempo, para os movimentos acelerados (quando a velocidade aumenta) e retardados (quando a velocidade diminui), são da seguinte forma:

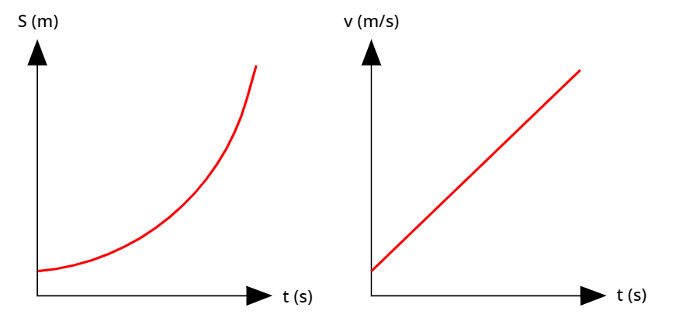
No movimento acelerado, o gráfico s(t) é uma parábola com a concavidade voltada para cima, enquanto v(t) é uma reta ascendente.

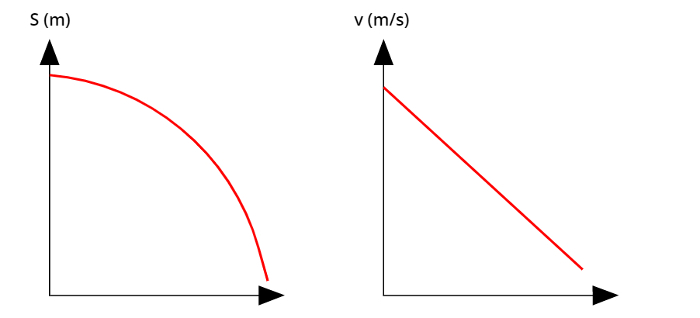
No movimento retardado, o gráfico s(t) é uma parábola com a concavidade voltada para baixo, enquanto v(t) é uma reta descendente.

Veja também: Saiba mais sobre os gráficos do movimento uniformemente variado

Aceleração escalar constante

Quando a aceleração de um móvel é constante, sua velocidade aumenta de forma igual, para intervalos de tempos iguais. Por exemplo, uma aceleração de 2 m/s² indica que a velocidade de um móvel aumenta em 2 m/s a cada segundo. A tabela a seguir apresenta dois móveis, 1 e 2, que se movem, respectivamente, com uma aceleração constante e uma aceleração variável:

Perceba que a velocidade do móvel 1 aumenta de forma constante a 2 m/s a cada segundo. Portanto, sua aceleração média é de 2 m/s², por isso dizemos que o seu movimento é uniformemente variado. No móvel 2, no entanto, a velocidade não muda de forma constante. Entre dois intervalos de tempos iguais, a sua velocidade muda de forma diferente, logo, dizemos que o seu movimento é variado.

Apesar de seu movimento ser variado, sua aceleração média é igual à aceleração média do móvel 1. Observe o cálculo:

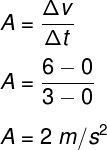
Apesar das suas acelerações médias serem iguais, os corpos 1 e 2 movem-se de forma diferente

É importante notar que a aceleração média apenas leva em conta os módulos final e inicial da velocidade, durante um certo período de tempo. Independentemente de como variou a velocidade, a aceleração média só será determinada pela diferença entre os valores de velocidade no início e no fim do movimento.

Cálculo do deslocamento com aceleração constante

Caso queiramos calcular o deslocamento de um móvel que tem sua velocidade alterada com uma aceleração constante, podemos utilizar as seguintes fórmulas:

Perceba que a fórmula dada acima pode ser usada quando sabemos por quanto tempo um móvel sofreu a aceleração. Caso não tivermos informação sobre qual foi o intervalo de tempo em que um movimento ocorreu, devemos utilizar a equação de Torricelli:

Aceleração escalar instantânea

Diferentemente da aceleração média, a aceleração instantânea determina a variação da velocidade a cada instante de um movimento. Para tanto, é necessário que o intervalo de tempo escolhido seja o menor possível. A fórmula abaixo traz a definição de aceleração escalar instantânea:

Portanto, a principal diferença entre as acelerações média e instantânea é o intervalo de tempo: a aceleração instantânea é calculada para intervalos de tempo pequenos, que tendam a zero.

Veja também: Dicas para resolver exercícios de Cinemática

Exercícios de aceleração escalar média

1) Um veículo tem sua velocidade alterada de acordo com o tempo conforme a tabela mostrada abaixo:

a) Calcule o módulo da aceleração média desse veículo entre os instantes t = 0 s e t = 3,0 s.

b) Calcule o espaço percorrido pelo veículo entre os instantes t = 0 s e t = 3,0 s.

c) Determine a função horária da velocidade desse veículo.

Resolução:

a) Para calcularmos a aceleração média do veículo, utilizaremos a fórmula de aceleração média. Observe:

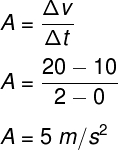
b) Vamos calcular o espaço percorrido pelo veículo por meio da sua função horária da posição:

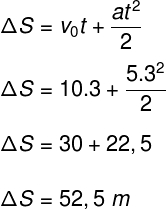
c) A função horária do movimento desse veículo pode ser determinada, se soubermos a sua velocidade inicial e a sua aceleração. Observe:

2) Um motorista dirige o seu veículo a 30 m/s, quando avista uma sinalização que indica que a velocidade máxima na via é de 20 m/s. Ao pisar no freio, o motorista reduz a velocidade até o valor indicado, deslocando-se cerca de 50 m entre o início e o final da frenagem. Determine o módulo da desaceleração que os freios do veículo imprimiram sobre ele.

Resolução:

Podemos calcular a desaceleração produzida pelos freios do veículo utilizando a equação de Torricelli, uma vez que não nos foi informado em qual intervalo de tempo ocorre a frenagem do veículo:

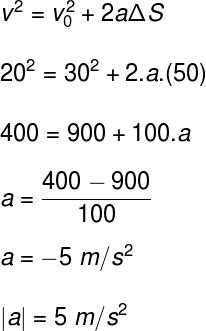
Por Me. Rafael Helerbrock