PUBLICIDADE
As relações trigonométricas se restringem somente a situações que envolvem triângulos retângulos.
Na situação abaixo, PÔR é um triângulo obtusângulo, então não podemos utilizar das relações trigonométricas conhecidas. Para situações como essa, utilizamos a lei dos senos ou a lei dos cossenos, de acordo com o mais conveniente.
Importante sabermos que:
sen x = sen (180º - x)
cos x = - cos (180º - x)
.jpg)
Lei dos senos
Resolvendo a situação da figura 1, temos:
Iremos aplicar a lei dos senos
.jpg)
Pela tabela de razões trigonométricas:
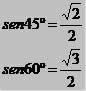
Lei dos cossenos
a² = b² + c² - 2*b*c*cosA
b² = a² + c² - 2*a*c*cosB
c² = a² + b² - 2*a*b*cosC
Exemplo
.jpg)
Analise o esquema abaixo:
Se optarmos pelo bombeamento da água direto para a casa, quantos metros de cano seriam gastos?
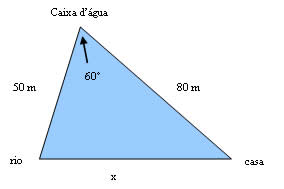
x² = 50² + 80² - 2*50*80*cos60º
x² = 2500 + 6400 – 8000*0,5
x² = 8900 – 4000
x² = 4900
x = 70 m
Seriam gastos 70 metros de cano.
Por Marcos Noé
Graduado em Matemática
Equipe Brasil Escola







.gif)