Os números ordinais, como o nome sugere, são os números que representam uma ordem. Os números ordinais representam posições em uma determinada sequência, como: primeiro, segundo, décimo quinto, entre outros.
Para representar um número ordinal, escrevemos os algarismos seguidos do símbolo °, por exemplo, o vigésimo é representado por 20°. A aplicação dos números ordinais é bastante recorrente em competições, em classificações e em demais situações em que é possível atribuir uma ordem para uma sequência de elementos.
Leia também: Propriedades dos números pares e ímpares
Tópicos deste artigo
- 1 - Resumo sobre os números ordinais
- 2 - O que são números ordinais?
- 3 - Notação dos números ordinais
- 4 - Escrita dos números ordinais
- 5 - Lista de números ordinais de 1 a 1000
- 6 - Tabela de números ordinais
- 7 - Diferença entre os números ordinais e cardinais
- 8 - Exercícios resolvidos sobre números ordinais
Resumo sobre os números ordinais
-
Os números ordinais são números que representam ordem.
-
Para representar um número ordinal, escrevemos os algarismos seguidos do símbolo ° ou ª.
-
Exemplos de números ordinais:
-
1º → primeiro
-
1ª → primeira
Anuncie aqui -
2º → segundo
-
2ª → segunda
-
10º → décimo
-
10ª → décima
-
-
Os números ordinais são utilizados em várias situações cotidianas envolvendo sequências.
O que são números ordinais?
Os números ordinais são utilizados no dia a dia para expressar a ordem de elementos em uma determinada sequência. Seu emprego é bastante comum para ordenar competidores ou elementos de um determinado conjunto, por exemplo: 1º (primeiro), no masculino, ou 1ª (primeira), no feminino. Os números ordinais são utilizados também para classificação, por exemplo, uma determinada peça de 1ª linha.
Notação dos números ordinais
Para representar um número ordinal, representamos o número seguido do símbolo º ou do símbolo ª.
Exemplos:
-
1º
-
3º
-
20ª
-
31ª
Anuncie aqui
Além da notação apresentada, existem outras bastante comuns, como o número seguido de um ponto final.
Exemplos
-
1.º
-
2.º
-
4.ª
-
10.ª
Anuncie aqui
Veja também: Como reconhecer os números primos?
Escrita dos números ordinais
Nosso sistema de numeração é representado por 10 símbolos, e, com base neles, conseguimos representar os demais números ordinais. Os nomes dos números ordinais por extenso são:
1º → primeiro
2º → segundo
3º → terceiro
4º → quarto
5º → quinto
6º → sexto
7º → sétimo
8º → oitavo
9º → nono
10º → décimo
Do 10º até o 19º, o nome é o termo décimo acompanhado do nome do algarismo da unidade:
11º → décimo primeiro
12º → décimo segundo
.
.
.
19º → décimo nono
Do 20º até o 29º, a lógica será a mesma:
20º → vigésimo
21º → vigésimo primeiro
.
.
.
29º → vigésimo nono
Lista de números ordinais de 1 a 1000
1º – primeiro
2º – segundo
3º – terceiro
4º – quarto
5º – quinto
6º – sexto
7º – sétimo
8º – oitavo
9º – nono
10º – décimo
11º – décimo primeiro
12º – décimo segundo
13º – décimo terceiro
14º – décimo quarto
15º – décimo quinto
16º – décimo sexto
17º – décimo sétimo
18º – décimo oitavo
19º – décimo nono
20º – vigésimo
21º – vigésimo primeiro
22º – vigésimo segundo
23º – vigésimo terceiro
24º – vigésimo quarto
25º – vigésimo quinto
26º – vigésimo sexto
27º – vigésimo sétimo
28º – vigésimo oitavo
29º – vigésimo nono
30º – trigésimo
40º – quadragésimo
50º – quinquagésimo
60º – sexagésimo
70º – septuagésimo
80º – octogésimo
90º – nonagésimo
100º – centésimo
200º – ducentésimo
300º – tricentésimo
400º – quadringentésimo
500º – quingentésimo
600º – sexcentésimo
700º – septingentésimo
800º – octingentésimo
900º – nongentésimo
1000º – milésimo
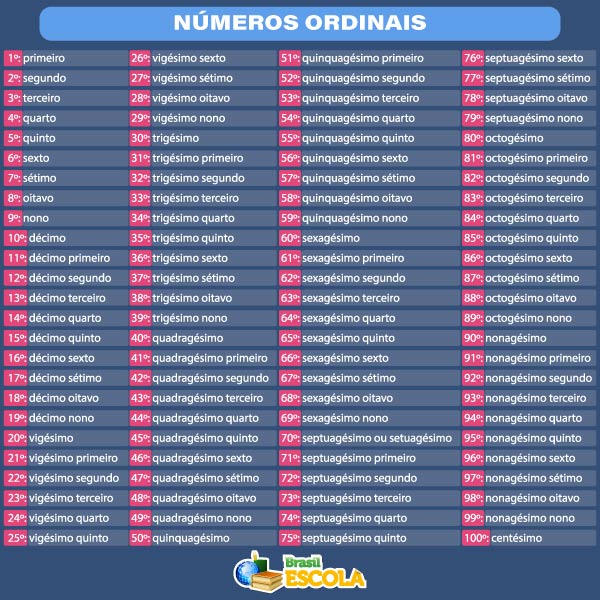
Tabela de números ordinais
Diferença entre os números ordinais e cardinais
Como vimos, os números ordinais representam ordem ou posição de determinados elementos que podem ser representados como uma sequência. Os números cardinais são utilizados para quantificar, ou seja, para representar quantidades absolutas ou contagens. Por exemplo: a quantidade de pessoas em um determinado evento e o número de acidentes de trânsito de uma cidade são quantificados como um número cardinal.
Exemplos:
-
10.325 pessoas compareceram ao evento.
Anuncie aqui -
Ocorreram 725 acidentes de trânsito na cidade X durante o ano.
Veja também: Números romanos – sistema de numeração representada por letras do alfabeto
Exercícios resolvidos sobre números ordinais
Questão 1 - Em uma corrida de Fórmula 1, o piloto brasileiro iniciou na 9ª posição. Durante a corrida, logo nas primeiras voltas, ele conseguiu ultrapassar 4 veículos até a última volta. Na última volta, ele conseguiu ultrapassar mais 1 de seus concorrentes e foi ultrapassado por 2 deles, então, a posição final desse piloto foi:
A) quinto lugar
B) sexto lugar
C) sétimo lugar
D) oitavo lugar
E) nono lugar
Resolução
Alternativa B
Ao ultrapassar 4 veículos, ele estava em 9º e foi para 5º. Depois, na última volta, ele chegou a ficar em 4º, mas foi ultrapassado por dois corredores, assumindo o 6º lugar, ou seja, ele terminou em 6º lugar.
Questão 2 - Ao analisar os meses do ano, qual é a posição ordinal dos meses de março e agosto nessa ordem:
A) terceiro e sexto meses
B) quarto e oitavo meses
C) segundo e décimo meses
D) sétimo e primeiro meses
E) terceiro e oitavo meses
Resolução
Alternativa E
Sabemos que março é o mês 3, logo, ele é o 3º (terceiro) mês do ano. Já agosto é o mês 8, ou seja, 8º (oitavo) mês.
Por Raul Rodrigues de Oliveira
Professor de Matemática

