Desvio-padrão

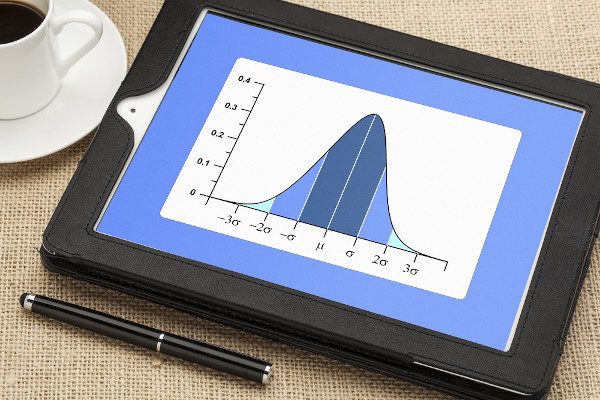
O desvio-padrão é uma medida de dispersão, assim como a variância e o coeficiente de variação. Ao determinar o desvio padrão, podemos estabelecer um intervalo em torno da média aritmética (divisão entre a soma dos números de uma lista e a quantidade de números somados) onde se concentra a maior parte dos dados. Quanto maior o valor do desvio-padrão, maior a variabilidade dos dados, ou seja, maior o afastamento em relação à média aritmética.

Leia também: Moda, média e mediana — as principais medidas de tendências centrais

Tópicos deste artigo

• 1 - Resumo sobre desvio-padrão
• 2 - O que é desvio-padrão?
• 3 - Como calcular o desvio-padrão?
• 4 - Quais são os tipos de desvio-padrão?
• 5 - Quais são as diferenças entre desvio-padrão e variância?
• 6 - Exercícios resolvidos sobre desvio-padrão

Resumo sobre desvio-padrão

• Desvio-padrão é uma medida de variabilidade.
• A notação do desvio-padrão é a letra grega sigma minúscula (σ) ou a letra s.
• O desvio-padrão é utilizado para verificar a variabilidade dos dados em torno da média.
• O desvio-padrão determina um intervalo \(\left[\mu-\sigma,\mu+\sigma\right]\), onde se encontra a maior parte dos dados.
• Para calcular o desvio-padrão, devemos encontrar a raiz quadrada da variância:

\(\sigma=\sqrt{\frac{\sum_{i=1}^{N}\left(x_i-\mu\right)^2}{N}}\)

O que é desvio-padrão?

O desvio-padrão é uma medida de dispersão adotada em Estatística. Seu uso está atrelado à interpretação da variância, que também é uma medida de dispersão.

Na prática, o desvio-padrão determina um intervalo, centrado na média aritmética, no qual a maior parte dos dados está concentrada. Desse modo, quanto maior o valor do desvio-padrão, maior a irregularidade dos dados (informações mais heterogêneas), e quanto menor o valor do desvio-padrão, menor a irregularidade dos dados (informações mais homogêneas).

Como calcular o desvio-padrão?

Para calcular o desvio-padrão de um conjunto de dados, devemos encontrar a raiz quadrada da variância. Assim, a fórmula para calcular o desvio-padrão é

\(\sigma=\sqrt{\frac{\sum_{i=1}^{N}\left(x_i-\mu\right)^2}{N}}\)

• \(x_1,x_2,x_3,\ldots,x_N\) → dados envolvidos.
• μ → média aritmética dos dados.
• N → quantidade de dados.
• \( \sum_{i=1}^{N}\left(x_i-\mu\right)^2\ =\ \left(x_1-\mu\right)^2+\left(x_2-\mu\right)^2+\left(x_3-\mu\right)^2+...+\left(x_N-\mu\right)^2 \)

O último item, que se se refere ao numerador do radicando, indica a soma dos quadrados da diferença entre cada dado e a média aritmética. Vale lembrar que a unidade de medida do desvio-padrão é a mesma unidade de medida dos dados x₁,x₂,x₃,…,x_N.

Ainda que a escrita dessa fórmula seja um pouco complexa, sua aplicação é mais simples e direta. Vejamos a seguir um exemplo de como utilizar essa expressão para calcular o desvio-padrão.

• Exemplo:

Durante duas semanas, foram registradas as seguintes temperaturas em uma cidade:

Em qual das duas semanas a temperatura se manteve mais regular nessa cidade?

Resolução:

Para analisar a regularidade da temperatura, devemos comparar os desvios-padrão das temperaturas registradas nas semanas 1 e 2.

• Vejamos inicialmente o desvio-padrão da semana 1:

Observe que a média μ₁ e N₁ são

\(\mu_1=\frac{29+30+31+31,5+28+28,5+29}{7}\approx29,57\)

\(N_1=7 \) (7 dias da semana)

Ainda, precisamos calcular o quadrado da diferença entre cada temperatura e a temperatura média.

\(\left(29-29,57\right)^2=0,3249\)

\(\left(30-29,57\right)^2=0,1849\)

\(\left(31-29,57\right)^2=2,0449\)

\(\left(31,5-29,57\right)^2=3,7249\)

\(\left(28-29,57\right)^2=2,4649\)

\(\left(28,5-29,57\right)^2=1,1449\)

\(\left(29-29,57\right)^2=0,3249\)

Somando os resultados, temos que o numerador do radicando na fórmula do desvio-padrão é

\(0,3249\ +\ 0,1849\ +2,0449+3,7249+2,4649+1,1449+0,3249\ =\ 10,2143\)

Assim, o desvio-padrão da semana 1 é

\(\sigma_1=\sqrt{\frac{\sum_{i=1}^{7}\left(x_i-\mu_1\right)^2}{N_1}}=\sqrt{\frac{10,2143}{7}}\ \approx1,208\ °C\)

Observação: Esse resultado significa que a maior parte das temperaturas da semana 1 se encontra no intervalo [28,36 °C, 30,77 °C], ou seja, o intervalo \(\left[\mu_1-\sigma_1,\mu_1+\sigma_1\right]\).

• Agora, vejamos o desvio-padrão da semana 2:

Seguindo o mesmo raciocínio, temos que

\(\mu_2=\frac{28,5+27+28+29+30+28+29}{7}=28,5\)

\(N_2=7\)

\(\left(28,5-28,5\right)^2=0\)

\(\left(27-28,5\right)^2=2,25\)

\(\left(28-28,5\right)^2=0,25\)

\(\left(29-28,5\right)^2=0,25\)

\(\left(30-28,5\right)^2=2,25\)

\(\left(28-28,5\right)^2=0,25\)

\(\left(29-28,5\right)^2=0,25\)

\(0\ +\ 2,25\ +\ 0,25\ +\ 0,25+2,25+0,25+0,25\ =\ 5,5\)

Logo, o desvio-padrão da semana 2 é

\(\sigma_2=\sqrt{\frac{\sum_{i=1}^{7}\left(x_i-\mu_1\right)^2}{N_2}}=\sqrt{\frac{5,5}{7}}\ \approx0,89\ °C\)

Esse resultado significa que a maior parte das temperaturas da semana 2 se encontra no intervalo \(\left[\mu_2-\sigma_2,\mu_2+\sigma_2\right]\), ou seja, o intervalo \(\left[\mu_2-\sigma_2,\mu_2+\sigma_2\right]\).

Perceba que \(\sigma_2<\sigma_1\), ou seja, o desvio-padrão da semana 2 é menor que o desvio-padrão da semana 1. Portanto, a semana 2 apresentou temperaturas mais regulares que a semana 1.

Quais são os tipos de desvio-padrão?

Os tipos de desvio-padrão estão relacionados com o tipo de organização dos dados. No exemplo anterior, trabalhamos com o desvio-padrão de dados não agrupados. Para calcular o desvio-padrão de um conjunto de dados organizados de outra maneira (dados agrupados, por exemplo), seria necessário ajustar a fórmula.

Quais são as diferenças entre desvio-padrão e variância?

O desvio-padrão é a raiz quadrada da variância:

\(\sigma=\sqrt{\frac{\sum_{i=1}^{N}\left(x_i-\mu\right)^2}{N}}\)

\(V=\frac{\sum_{i=1}^{N}\left(x_i-\mu\right)^2}{N}\)

Ao utilizar a variância para determinar a variabilidade de um conjunto de dados, o resultado possui a unidade dos dados elevada ao quadrado, o que dificulta sua análise. Assim, o desvio-padrão, que possui a mesma unidade dos dados, é uma possível ferramenta para interpretar o resultado da variância.

Saiba mais: Frequência absoluta — o número de vezes que uma mesma resposta apareceu durante a coleta de dados

Exercícios resolvidos sobre desvio-padrão

Questão 1

(FGV) Em uma turma de 10 alunos, as notas dos alunos em uma avaliação foram:

O desvio-padrão dessa lista é, aproximadamente,

A) 0,8.

B) 0,9.

C) 1,1.

D) 1,3.

E) 1,5.

Resolução:

Alternativa C.

Segundo o enunciado, N = 10. A média dessa lista é

\( \mu=\frac{6+7+7+8+8+8+8+9+9+10}{10}=8 \)

Além disso,

\(\left(6-8\right)^2=4\)

\(\left(7-8\right)^2=1\)

\(\left(8-8\right)^2=0\)

\(\left(9-8\right)^2=1\)

\(\left(10-8\right)^2=4\)

\(4+1+1+0+0+0+0+1+1+4=12\)

Portanto, o desvio-padrão dessa lista é

\(\sigma=\sqrt{\frac{\sum_{i=1}^{10}\left(x_i-8\right)^2}{10}}=\sqrt{\frac{12}{10}}\approx1,1\)

Questão 2

Considere as afirmações abaixo e classifique cada uma como V (verdadeira) ou F (falsa).

I. A raiz quadrada da variância é o desvio-padrão.

II. O desvio-padrão não possui relação com a média aritmética.

III. A variância e o desvio-padrão são exemplos de medidas de dispersão.

A ordem correta, de cima para baixo, é

A) V-V-F

B) F-F-V

C) F-V-F

D) V-F-F

E) V-F-V

Resolução:

Alternativa E.

I. A raiz quadrada da variância é o desvio-padrão. (verdadeira)

II. O desvio-padrão não possui relação com a média aritmética. (falsa)
O desvio-padrão indica um intervalo em torno da média aritmética no qual a maior parte dos dados se encontram.

III. A variância e o desvio-padrão são exemplos de medidas de dispersão. (verdadeira)

 

Por Maria Luiza Alves Rizzo
Professora de Matemática