Energia interna é a soma das energias cinética e potencial relacionadas ao movimento dos átomos e moléculas constituintes de um corpo. A energia interna também é diretamente proporcional à temperatura do corpo. Trata-se de uma grandeza escalar medida em Joules (SI) e determinada em função de variáveis como pressão (P), volume (V) e temperatura termodinâmica (T) de um sistema, em Kelvin (K).
Quanto maior for a temperatura de um corpo, maior será a sua energia interna, portanto, maior será a sua capacidade de realizar algum trabalho. Além disso, a energia interna de gases monoatômicos, por exemplo, é dada exclusivamente pela soma da energia cinética de cada átomo do gás. Quando lidamos com gases moleculares, como os gases diatômicos, deve-se levar em conta as interações moleculares e, por isso, a energia interna é determinada pela soma da energia cinética das moléculas com a energia potencial existente entre elas.
Tópicos deste artigo
- 1 - Energia interna de gases monoatômicos ideais
- 2 - Energia interna para gases diatômicos
- 3 - Energia interna em transformações e ciclos termodinâmicos
- 4 - Energia interna em processos cíclicos
- 5 - Exercícios sobre energia interna
Energia interna de gases monoatômicos ideais
Como não existe interação entre os átomos de um gás monoatômico ideal, sua energia interna depende exclusivamente de duas variáveis: o número de mols (n) e a temperatura do gás (T). Observe:
![]()
U – energia interna
n – número de mols
R – constante universal dos gases perfeitos
T – temperatura
Na equação acima, R tem módulo de 0,082 atm.L/mol.K ou 8,31 J/mol.K (SI). Além disso, podemos escrever a equação acima em termos de outras grandezas, como a pressão e o volume. Para tanto, precisamos recordar a Equação de Clapeyron, usada para os gases ideais.
![]()
Substituindo a equação acima na anterior, teremos a seguinte expressão para o cálculo da energia interna:
![]()
Veja também: O que é um gás perfeito?
Levando-se em conta as equações acima, é possível determinar uma relação entre a energia cinética dos átomos de um gás monoatômico ideal e a sua temperatura. Para isso, afirmaremos que a energia cinética desse tipo de gás é puramente cinética. Observe:
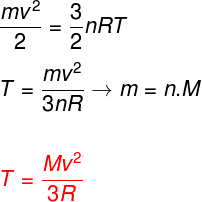
m – massa
n – número de mol
M – massa molar
Em diversas situações, é interessante saber calcular a variação da energia interna (ΔU) de um gás, pois essa grandeza indica se o gás recebeu ou cedeu energia. Caso a variação da energia interna do gás tenha sido positiva (ΔU > 0), o gás terá recebido energia; caso contrário (ΔU< 0), o gás terá cedido parte de sua energia.
![]()
Variação da energia interna em termos da variação de volume do gás.
Energia interna para gases diatômicos
Para os gases diatômicos ideais, a energia interna é dada por uma equação um pouco diferente.
![]()
Energia interna em transformações e ciclos termodinâmicos
De acordo com a 1ª Lei da Termodinâmica, a energia interna de um gás ideal pode sofrer variações em determinadas transformações termodinâmicas, dependendo da quantidade de calor trocada entre as vizinhanças e o sistema, bem como do trabalho realizado por ou sobre o sistema.
![]()
Q – calor
τ - trabalho
Em seguida, vamos conferir a forma que essa lei assume para algumas transformações termodinâmicas particulares.
Veja também: História das máquinas térmicas
→ Energia interna: transformação isotérmica
Na transformação isotérmica, não há mudança de temperatura e, por isso, a energia interna permanece constante.
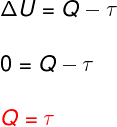
Nesse caso, toda a quantidade de calor que é trocada com o sistema é transformada em trabalho e vice-versa.
→ Energia interna: transformação isovolumétrica
Na transformação isovolumétrica, não é possível haver realização de trabalho, uma vez que o sistema encontra-se confinado em um recipiente rígido e inexpansível. Nesse caso, toda a quantidade de calor que é trocada com o sistema varia diretamente sua energia interna.
![]()
→ Energia interna: transformação isobárica
Nesse tipo de transformação, o sistema está submetido a uma pressão constante, logo, o trabalho por ele ou sobre ele realizado pode ser calculado analiticamente.
![]()
→ Energia interna: transformação adiabática
Nas transformações adiabáticas, não ocorrem trocas de calor entre o sistema e a sua vizinhança, portanto, a variação da energia interna depende exclusivamente do trabalho realizado por ou sobre o sistema.
![]()
Energia interna em processos cíclicos
Em todo processo cíclico, o estado termodinâmico de um sistema, representado por suas variáveis pressão, volume e temperatura (P, V, T), é transformado, mas acaba retornando ao estado original (P,V,T), portanto, a variação de energia interna nesse tipo de processo é sempre nula (ΔU = 0).
Veja também: Transformações cíclicas
Observe o gráfico a seguir, no qual aparecem três transformações termodinâmicas distintas entre os estados A e B.
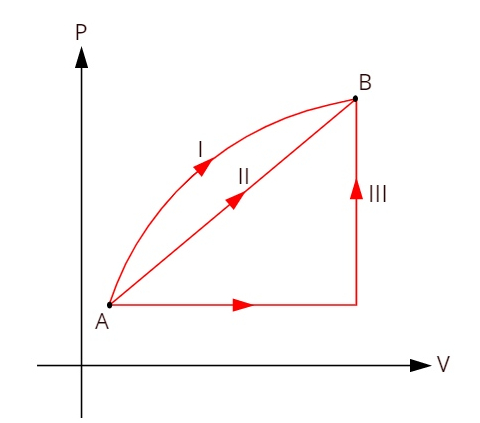
Como as três transformações (I, II e III) saem do estado A e vão para o estado B, a variação de energia interna deve ser igual para todas elas, portanto:
![]()
Exercícios sobre energia interna
1) Dois mols de um gás diatômico ideal, de massa molar igual a 24 g/mol, encontram-se em uma temperatura de 500 K dentro de um recipiente fechado e rígido de volume igual a 10-3 m³. Determine:
a) O módulo da energia interna desse gás em joules.
b) A pressão que o gás exerce sobre as paredes do recipiente.
Resolução:
a) Em se tratando de um gás diatômico e ideal, utilizaremos a fórmula abaixo para calcular sua energia interna:
![]()
Tomando os dados que foram informados no enunciado do exercício, teremos o seguinte cálculo a ser resolvido:
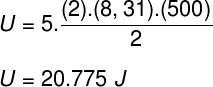
b) Podemos determinar a pressão que o gás exerce, uma vez que conhecemos o volume do seu recipiente: 10-3 m³. Para tanto, usaremos a fórmula a seguir:
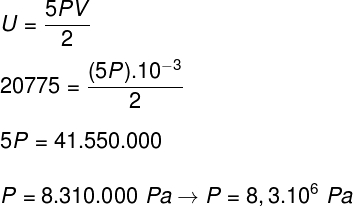
Por Me.Rafael Helerbrock
