PUBLICIDADE
Quando estamos trabalhando com Trigonometria e deparamo-nos com um ângulo que não se encontra no primeiro quadrante, sempre podemos reduzi-lo de forma a encontrar o ângulo correspondente a esse que esteja justamente no 1° quadrante. Isso é possível graças à simetria presente no ciclo trigonométrico. Mas precisamos nos atentar para o que ocorre com os sinais das funções trigonométricas em cada quadrante. Vejamos a seguir algumas formas de trabalhar a mudança de quadrante no ciclo trigonométrico.
Redução ao Primeiro Quadrante
Na figura a seguir, considere o ângulo x, destacado em vermelho no primeiro quadrante. Nós podemos encontrar os ângulos que são correspondentes a x nos demais quadrantes. A distância desses ângulos a x é sempre um valor múltiplo de 90°, de modo que o módulo das funções trigonométricas desses ângulos não se altera.
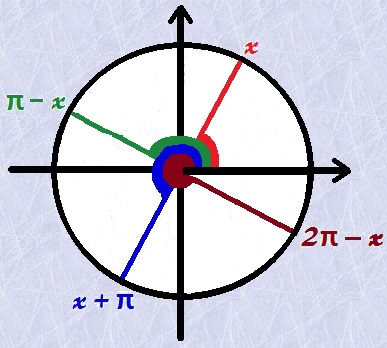
Método prático para redução ao primeiro quadrante
Se o ângulo com o qual estamos trabalhando for y e ele estiver no segundo quadrante, seu correspondente no 1° quadrante será o ângulo x tal que π – x = y ou 180° – x = y.
Exemplo 1:
Considere o ângulo 150°. Para reduzi-lo ao 1° quadrante, teremos o seguinte:
180° – x = 150°
x = 30°
Analogamente, se o ângulo y pertencer ao terceiro quadrante, seu correspondente x no primeiro quadrante será dado por x + π = y ou 180° + x = y.
Exemplo 2:
Considere o ângulo 4π/3, seu correspondente será:
x + π = 4π
3
x = 4π – π
3
x = π
3
Por fim, se o ângulo analisado y pertencer ao quarto quadrante, o ângulo x correspondente a ele no primeiro quadrante será dado por 2π – x = y ou 360° – x = y.
Exemplo 3:
Considere o ângulo 300°, reduzindo-o ao primeiro quadrante, teremos:
360° – x = 300°
x = 60°
Vale lembrar que os ângulos correspondentes possuem valores parecidos de seno, cosseno e tangente, e a distinção ocorre pelo sinal. No primeiro quadrante, os valores de seno, cosseno e tangente são positivos. No segundo quadrante, o seno é positivo, enquanto o cosseno e a tangente são negativos. No terceiro quadrante, seno e cosseno são negativos, enquanto a tangente é positiva. No quarto quadrante, seno e tangente são negativos, e o cosseno é positivo. Podemos ver a distinção entre os sinais na imagem a seguir:
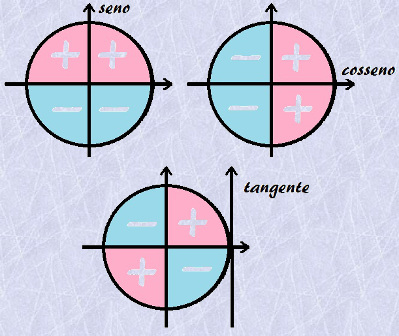
Confira os sinais das funções trigonométricas de acordo com o quadrante
Por Amanda Gonçalves
Graduada em Matemática






