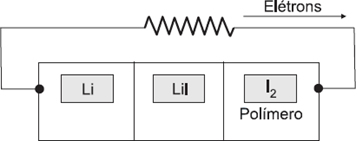
Considere duas pilhas envolvendo o eletrodo de cobre:
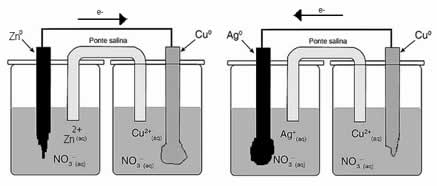
Pilhas zinco-cobre e cobre-prata.
Na primeira pilha, conhecida como pilha de Daniell, os eletrodos são de zinco e de cobre e notamos que o zinco sofre oxidação, ou seja, doa elétrons para o cobre, sendo, portanto, o ânodo. O eletrodo de cobre, por sua vez, funciona como o cátodo, recebendo elétrons e se reduzindo.
Entretanto, é possível observar que na segunda pilha, a de eletrodos cobre-prata, o cobre funciona não como cátodo, mas como ânodo, oxidando desta vez.
Isso nos mostra que comparando esses três eletrodos, a tendência de sofrer redução funciona da seguinte maneira:
| Zinco < Cobre < Prata |
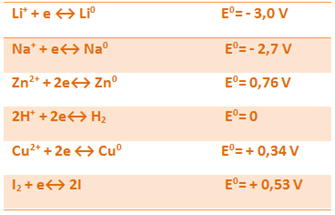
Assim, essa capacidade de sofrer redução é chamada de Potencial de Redução (Ered). Visto que esse valor depende da pressão, temperatura e concentração da solução, determinou-se um potencial-padrão (ou normal, em 25°C, pressão de 1atm, e concentração de 1,0 mol/L) que é identificado pelo símbolo E0. O contrário também é verdadeiro, existe o Potencial de Oxidação (Eóxi), que nesse caso tem a ordem crescente:
| Zinco > Cobre > Prata |
Quanto menor o potencial-padrão de redução, maior a capacidade que o metal possui de doar elétrons e vice-versa. De maneira similar, quanto menor o potencial-padrão de oxidação, maior a capacidade que o metal possui de receber os elétrons e vice-versa.
| Em uma pilha, a espécie que apresenta maior Ered sofre redução e a outra espécie, de maior Eóxi, sofre oxidação. |
Se adaptarmos um voltímetro, como o da figura acima, em uma dessas pilhas, será medida a intensidade da corrente elétrica produzida por elas, isto é, a sua força eletromotriz (fem ou E) ou diferença de potencial (U ou ddp)*. O valor é indicado em volts (V), aparecendo normalmente nas embalagens e rótulos das pilhas.
.jpg)
Diferença de potencial (U ou ddp) de uma pilha mostrada no rótulo.
A força eletromotriz pode ser expressa em termos de potencial de redução ou de oxidação. É importante lembrar que esses potenciais têm o mesmo valor, porém possuem sinais contrários.
Para calcularmos a voltagem de uma pilha no estado padrão, usamos a seguinte expressão:
| ∆E0 = E0red (cátodo) - E0 red (ânodo) |
ou
| ∆E0 = E0oxi (ânodo) - E0 oxi (cátodo) |
Desse modo, os valores absolutos de cada eletrodo não aparecem no voltímetro, mas sim a diferença de potencial entre eles.
*Consideramos a diferença de potencial igual à força eletromotriz, porque o cálculo da diferença de potencial de um gerador é dado pela equação: U = E – r.i, onde:
U = diferença de potencial
E = força eletromotriz
r = resistência interna
i= intensidade da corrente elétrica
Mas, na Química, consideramos as pilhas como geradores ideais, de modo que sua resistência interna seja desprezível em relação ao circuito elétrico. Dessa maneira, temos que U = E.