Sistema em rotação – momento de inércia

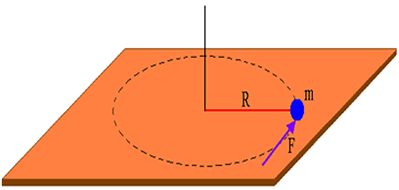
De acordo com a Segunda Lei de Newton, quando aplicamos uma força sobre um objeto que contém massa, este adquire aceleração. Para um corpo em movimento circular, isto é, para um corpo em rotação, podemos determinar sua posição e velocidade em função de variáveis como o ângulo e a velocidade angular, além do raio da trajetória.

Vejamos a figura acima, nela temos um corpo de massa m que está preso a um eixo central, que gira em uma trajetória circular cujo raio vale R. Vamos analisar esse movimento. Ainda com relação à figura acima, suponhamos que uma força de intensidade F atue sempre na direção da velocidade tangencial v do corpo de massa m. Podemos escrever a Segunda Lei de Newton para os módulos das grandezas:

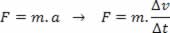
Como a velocidade linear de um movimento circular é dada por v = ω.R, podemos escrever a equação acima da seguinte forma:

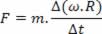
Multiplicando ambos os lados por R, teremos:

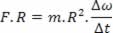
Sabendo que o quociente entre a velocidade angular e o tempo nos fornece a aceleração angular, temos:

F.R=m.R².α

Lembrando que a força é perpendicular ao raio da trajetória, vemos que F.R = M é o módulo do torque exercido pela força F em relação ao centro do movimento circular. Temos como resultado:

M = m.R².α   ⟹   M = I.α

Onde I = m.R².

A equação M = I.α relaciona o módulo do torque M com a aceleração angular α e com a quantidade I que representa a inércia rotacional do objeto. A quantidade I é conhecida como o momento de inércia do corpo e a sua unidade no SI é kg.m².

Nesse exemplo, chegamos à conclusão de que o momento de inércia relaciona-se tanto com a massa, como também com o raio da trajetória circular. A equação do momento de inércia permite calcular o momento de qualquer corpo, sendo assim, podemos dizer que a equação do momento de inércia (M = I.α) é equivalente a Segunda Lei de Newton para objetos sujeitos a torque.

Por Domiciano Marques
Graduado em Física