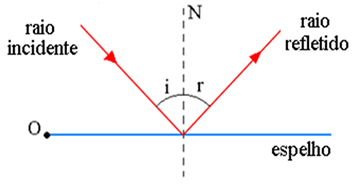
Em nossos estudos sobre espelhos planos vimos que eles são superfícies planas polidas que refletem a imagem de um objeto. De acordo com a lei da reflexão, o raio incidente, a reta normal à superfície plana do espelho e o raio refletido pertencem ao mesmo plano e o ângulo incidente é congruente ao ângulo de reflexão.
Sendo assim, um espelho plano conjuga uma imagem virtual, direita e de mesmo tamanho do objeto, sendo essa imagem posicionada simetricamente ao objeto em relação ao plano do espelho, isto é, a imagem possui a mesma distância do espelho em relação à distância do objeto ao espelho. Vejamos a figura acima: nela temos um raio de luz que incide sobre a superfície plana do espelho fixo no ponto O. Podemos ver que o raio é refletido seguindo exatamente a segunda lei da reflexão.
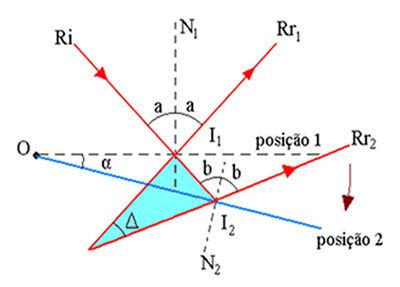
Veja a figura acima: nela podemos ver que na posição 1 temos um raio de luz incidente (Ri) e que Rr1 é o raio refletido. Se fizermos o espelho girar sobre o ponto fixo O um ângulo α vemos que o mesmo raio incidente Ri individualiza o raio refletido Rr2, agora com o espelho na posição 2, conforme ilustra a figura acima.
De acordo com a figura, temos, para a trajetória descrita pelo raio, que:
I1 é o ponto onde o raio luminoso incide no espelho, na posição 1;
I2 é o ponto onde o raio luminoso incide no espelho, exatamente na posição 2;
α é o ângulo de rotação do espelho plano, na posição fixa;
Δ é o ângulo de rotação dos raios refletidos, isto é, é o ângulo entre Rr1 e Rr2;
I é o ponto de interseção entre os prolongamentos dos raios de reflexão e incidência na segunda posição do espelho.
Como a soma dos ângulos internos de um triangulo é igual a 180º, temos:
∆+2a+(180°-2b)=180°
∆ =2b-2a
∆ =2(b-a)(I)
α=b-a (II)
Substituindo (II) em (I), temos:
∆ =2α
Sendo assim, podemos definir que o ângulo de rotação dos raios refletidos é o dobro do ângulo de rotação do espelho.
Por Domiciano Marques
Graduado em Física
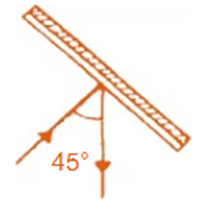 b)
b) 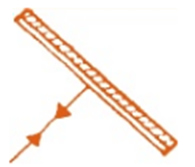 c)
c) 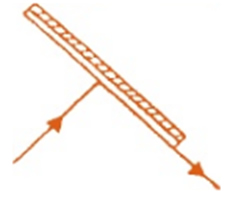
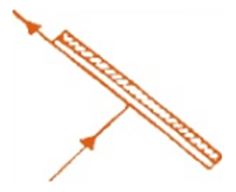 e)
e)