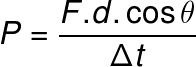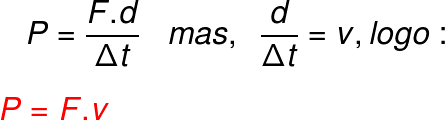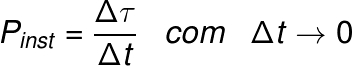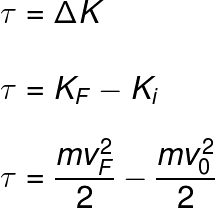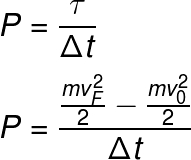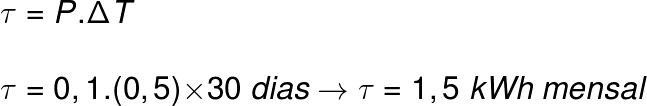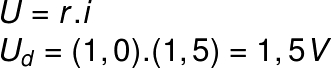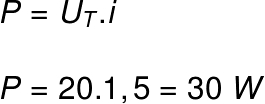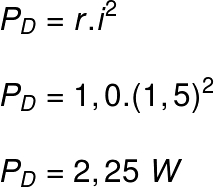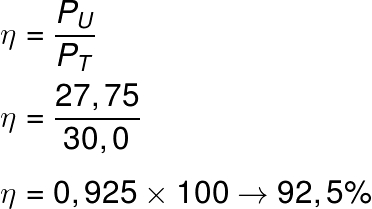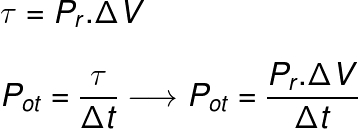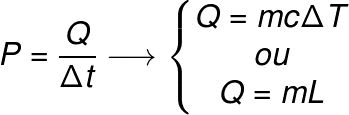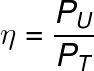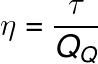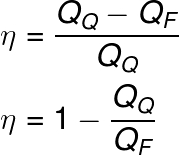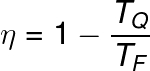Potência é uma grandeza física escalar medida em watts (W). Pode ser definida como a taxa de realização de trabalho a cada segundo ou como o consumo de energia por segundo. O watt, unidade de potência do sistema internacional de unidades (SI), equivale a 1 joule por segundo.
Veja também: O que é trabalho mecânico?
Tópicos deste artigo
- 1 - Resumo sobre potência e rendimento
- 2 - O que é potência na Física?
- 3 - Cálculo da potência
- 4 - Potência mecânica
- 5 - Potência elétrica
- 6 - Exemplo
- 7 - Exercício resolvido de potência elétrica e rendimento
- 8 - Resolução
- 9 - Potência Termodinâmica
- 10 - Rendimento
- 11 - Rendimento de uma máquina
Resumo sobre potência e rendimento
-
Potência é a taxa de variação da quantidade de energia fornecida ou cedida por um sistema durante um intervalo de tempo.
-
A unidade de potência no sistema internacional de unidades (SI) é o watt: 1 watt equivale a 1 joule por segundo.
-
Se uma máquina é capaz de realizar o mesmo trabalho que outra em um tempo menor, sua potência é considerada maior que a da outra máquina.
-
O rendimento de um sistema é dado pela razão entre a potência útil e a potência total.
-
A potência não útil para o sistema é chamada de potência dissipada.
O que é potência na Física?
Potência é uma grandeza física usada para calcular a quantidade de energia concedida ou consumida por unidade de tempo. Em outras palavras, é a taxa de variação da energia em função do tempo. A potência é útil par medir a rapidez com a qual uma forma de energia é transformada por meio da realização de um trabalho.
| Dizemos que uma máquina é mais potente que outras máquinas quando ela é capaz de realizar a mesma tarefa em um tempo menor ou, ainda, realizar uma quantidade maior de tarefas no mesmo intervalo de tempo. |
A definição de potência média é dada pelo trabalho realizado em função da variação de tempo:
Legenda:
P – potência média (W)
τ – trabalho (J)
Δt – intervalo de tempo (s)
A unidade de medida da potência adotada pelo SI é o watt (W), unidade equivalente ao joule por segundo (J/s). A unidade watt foi adotada a partir de 1882 como forma de homenagem aos trabalhos desenvolvidos por James Watt, que foram de extrema relevância para o desenvolvimento das máquinas a vapor.
Na Física, trabalho é a medida da transformação de uma forma de energia em outras formas de energia mediante a aplicação de uma força. Sendo assim, a definição de potência pode estar relacionada com qualquer forma de energia, tais como: energia mecânica, energia potencial elétrica e energia térmica.
Cálculo da potência
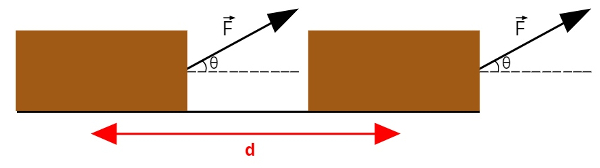
Podemos determinar a potência realizada pela aplicação de uma força F que desloca um corpo de massa m em uma distância d. Observe:
Na situação descrita acima, podemos calcular a potência do movimento por meio da definição de potência média:
Para tanto, precisamos recordar que o trabalho realizado por uma força F pode ser calculado por meio da seguinte fórmula:
Legenda:
F – força aplicada (N)
d – distância percorrida (m)
θ – ângulo formado entre F e d (º)
Reunindo as duas equações anteriores em uma só, teremos a seguinte equação para o cálculo da potência relacionada a uma forma de energia qualquer:
Para os casos em que a força aplicada é paralela à distância percorrida pelo corpo, o cosseno do ângulo θ terá seu valor máximo (cos 0º = 1). Portanto, a potência média poderá ser calculada a partir da seguinte relação:
Legenda:
v – velocidade do corpo (m/s)
De acordo com o cálculo demonstrado acima, é possível calcular a potência com a qual a energia presente em um corpo é transformada. Isso é possível se soubermos o módulo da força resultante, que deverá ser multiplicado pela velocidade média percorrida pelo corpo ao longo de um percurso de distância d. No entanto, é necessário lembrar que a definição apresentada acima só é válida para valores constantes de F.
Veja também: Exercícios sobre potência mecânica e rendimento
→ Potência instantânea
Potência instantânea é a medida da quantidade de trabalho realizado em um processo durante um intervalo de tempo muito pequeno (infinitesimal). Podemos dizer, portanto, que a potência instantânea é a taxa de variação da quantidade de trabalho durante um intervalo de tempo que tende a zero.
Legenda:
Pinst – potência instantânea (W)
Δτ – trabalho infinitesimal (J)
Δt – intervalo de tempo infinitesimal (s)
A potência instantânea é usada para calcular a taxa de realização de trabalho a cada instante, não durante um longo processo. Por isso, quanto menores os intervalos de tempo Δt, mais precisas serão as aferições da potência instantânea.
Potência mecânica
Potência mecânica é definida como a taxa de variação das formas de energia relacionadas ao estado de movimento de um corpo. Podemos calcular a potência mecânica de um corpo em movimento por meio das variações de sua energia cinética e de sua energia potencial (gravitacional ou elástica, por exemplo). A potência associada à transformação da energia mecânica, entretanto, só se aplica a sistemas dissipativos (que apresentam atrito), uma vez que, na ausência de atrito e de outras forças dissipativas, a energia mecânica dos corpos mantém-se constante.
De acordo com o Teorema do Trabalho-Energia, é possível calcular a quantidade de trabalho aplicado a um corpo pela variação da energia cinética por ele obtida.
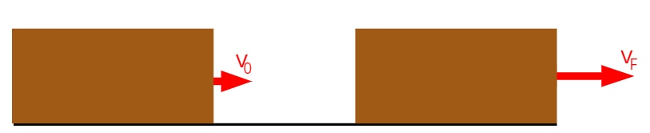
O corpo de massa m ilustrado na figura abaixo é acelerado pela ação de uma força F, tendo sua velocidade variada de v0 até vF:
Legenda:
v0 – velocidade inicial (m/s)
vF – velocidade final (m/s)
De acordo com o Teorema Trabalho-Energia, o trabalho realizado sobre o corpo é dado por:
Legenda:
ΔK – variação da energia cinética (J)
KF – energia cinética final (J)
KI – energia cinética inicial (J)
m – massa do corpo (kg)
Dessa forma, a potência mecânica relacionada a esse movimento pode ser calculada por meio da seguinte equação:
Potência elétrica
A potência elétrica é uma importante medida que deve ser analisada ao adquirirmos algum eletrodoméstico. A potência elétrica de qualquer dispositivo mede a quantidade de energia elétrica que o aparelho é capaz de transformar em outras formas de energia a cada segundo. Por exemplo, um liquidificador de 600 W é capaz de transformar 600 J de energia elétrica a cada segundo em energia cinética, transmitindo calor, vibração e ondas sonoras para suas pás.
Como sabemos, de forma geral, a potência pode ser calculada por meio da razão entre o trabalho realizado e o intervalo de tempo decorrido durante sua realização. Portanto, utilizaremos aqui a definição de trabalho realizado pela força elétrica:
.jpg)
Legenda:
τFel – trabalho da força elétrica (J)
q – módulo da carga elétrica (C )
ΔU – diferença de potencial (V)
P – potência elétrica (W)
UB e UA – tensão elétrica nos pontos A e B (V)
Δt – intervalo de tempo de movimento da carga (s)
i – módulo da corrente elétrica (A)
A potência elétrica funciona da seguinte forma: quando ligamos um aparelho na tomada, forma-se uma diferença de potencial (ΔU) entre seus terminais. Quando uma diferença de potencial (ΔU) é aplicada sobre um material condutor, uma quantidade de trabalho (τFel) é realizada sobre as cargas elétricas (q) nos circuitos do aparelho, fazendo com que essas cargas movam-se, ou seja, atribuindo-lhes energia cinética. A movimentação das cargas em uma direção preferencial é chamada de corrente elétrica (i). A potência elétrica (P), por sua vez, é a medida da quantidade de trabalho (τFel) que foi realizada pelas cargas a cada segundo (Δt) de funcionamento do dispositivo.
O consumo de energia elétrica, portanto, é determinado pela potência dos aparelhos ligados à rede elétrica e pelo seu tempo de funcionamento.
Além da fórmula citada acima, existem variações que podem ser escritas a partir da 1ª Lei de Ohm. São elas:
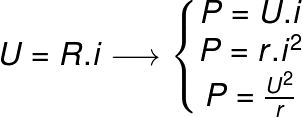
Três maneiras possíveis de se calcular potência elétrica
Legenda:
U – potencial elétrico (V)
r – resistência elétrica (Ω)
Veja também: Potência dissipada em um resistor
→ Consumo de energia elétrica
A quantidade de energia elétrica consumida é medida em uma unidade chamada de quilowatt-hora (kWh). Essa é uma unidade alternativa para a unidade de energia do sistema internacional de unidades, o joule. O quilowatt-hora é usado em virtude de sua praticidade. Se a energia elétrica fosse medida em joules, os números utilizados para expressar seu consumo seriam enormes e pouco práticos.
Um quilowatt-hora é a quantidade de energia consumida (ou o trabalho realizado) por um aparelho de 1000 W (1 kW) durante o intervalo de tempo de 1h (3600 s). Multiplicando essas quantidades, chegamos à conclusão de que cada quilowatt-hora equivale a 3,6.106 J (três milhões e seiscentos mil joules).
Para calcularmos o consumo de um aparelho eletroeletrônico, basta multiplicarmos sua potência pelo seu tempo de funcionamento.
Exemplo
Considere um aparelho de potência igual a 100 W (0,1 kW) que opere durante 30 minutos por dia (0,5 h). Qual será seu consumo mensal (30 dias) de energia elétrica?
De acordo com nosso cálculo, esse aparelho consumirá 1,5 kWh mensal, o equivalente a 5,4.106 J. Se o kWh da região custar R$ 0,65, o preço a ser pago no final do mês pelo funcionamento desse aparelho será de R$ 0,97.
Veja também: Geradores elétricos e força eletromotriz
Exercício resolvido de potência elétrica e rendimento
Quando conectada a um circuito, uma bateria de força eletromotriz igual a 20,0 V e resistência interna de 1,0 Ω produz uma corrente elétrica de 1,5 A. Em relação a essa bateria, determine:
a) A diferença de potencial elétrico estabelecida entre os terminais desse resistor.
b) A potência elétrica fornecida pela bateria.
c) A potência elétrica dissipada pela resistência interna da bateria.
d) O rendimento dessa bateria.
Resolução
Inicialmente, listaremos os dados fornecidos pelo exercício.
Dados:
-
UT = 20,0 V – força eletromotriz da bateria ou potencial total
-
r = 1,0 Ω – resistência interna da bateria
Anuncie aqui -
i = 1,5 A – corrente elétrica
a) Para determinar a diferença de potencial formada entre as extremidades do resistor, usamos a 1ª lei de Ohm.
Legenda:
UD – Tensão elétrica dissipada no resistor (V)
b) A potência elétrica fornecida pela bateria pode ser calculada por meio da fórmula abaixo:
Legenda:
UT – tensão elétrica total ou força eletromotriz da bateria (V)
c) Vamos calcular a potência elétrica dissipada pelo resistor. Para isso, basta usarmos uma das fórmulas de potência que já conhecemos:
Legenda:
PD – potência dissipada (W)
d) O rendimento desse gerador pode ser calculado por meio da razão entre a potência utilizável e a potência total da bateria. A partir dos cálculos realizados nos itens anteriores, determinamos que a potência total fornecida pela bateria era de 30 W, enquanto a potência dissipada por sua resistência interna era de 2,25 W. Portanto, a potência utilizável é dada pela diferença entre essas duas potências e vale 27,75 W. Fazendo a razão entre a potência utilizável e a potência total, teremos:
De acordo com o cálculo realizado, o rendimento energético da bateria é de 92,5 %.
Potência Termodinâmica
A potência termodinâmica pode ser calculada por meio da determinação da quantidade de trabalho que é realizada por (ou sobre) um gás durante sua expansão ou compressão isobárica (pressão constante) durante um intervalo de tempo.
Também é possível calcular a potência de uma fonte de calor relacionando a quantidade de calor sensível ou latente emitida por intervalo de tempo.
→ Potência do trabalho realizado pelo gás
Nas transformações isobáricas, é possível determinar a potência fornecida ou cedida por um gás. Para tanto, precisamos levar em conta a fórmula utilizada para calcular o trabalho termodinâmico envolvido em uma transformação isobárica:
Legenda:
Pr – pressão (Pa)
Pot – potência (W)
ΔV – variação de volume (m³)
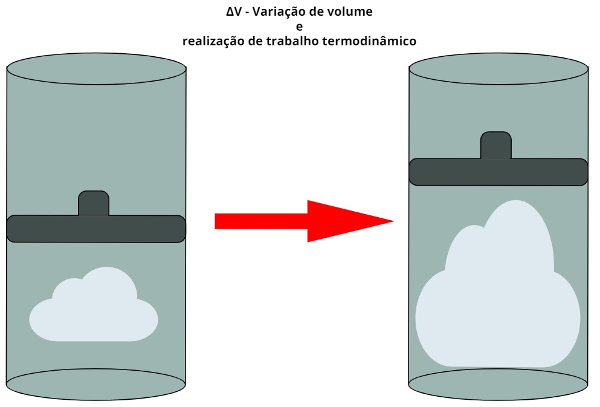
Nas transformações termodinâmicas isobáricas, o gás converte parte de sua energia interna em trabalho ao empurrar um pistão.
Veja também: A história das máquinas térmicas
→ Potência e calor
Podemos determinar a potência fornecida por uma chama ou a potência emitida por um resistor aquecido em decorrência do efeito Joule por meio do cálculo da quantidade de calor dissipado por essas fontes a cada segundo. Para tanto, basta fazermos o seguinte cálculo:
Para calcularmos a potência emitida por uma fonte em forma de calor, basta determinarmos se esse calor é do tipo sensível (Q = mcΔT) ou do tipo latente (Q = mL). Esses calores estão presentes, exclusivamente, nas mudanças de temperatura e nas mudanças de estado físico, respectivamente.
Rendimento
Rendimento é uma importante variável para o estudo de sistemas não conservativos, isto é, que apresentam perdas de energia, como nos casos não ideais do nosso dia a dia. Todas as máquinas e aparelhos que conhecemos são sistemas incapazes de aproveitar toda a potência fornecida a eles. Assim, “desperdiçam” parte da potência em outras formas de energia menos úteis, como calor, vibração e ruídos.
Uma das definições mais gerais de rendimento pode ser dada pela divisão da potência útil pela potência total recebida durante algum processo:
Legenda:
η – rendimento
PU – potência útil (W)
PT – potência total (W)
Rendimento de uma máquina
O rendimento das máquinas térmicas mede sua eficiência energética, ou seja, a porcentagem de energia que essas máquinas são capazes de aproveitar para realizar trabalho útil (τ). Todas as máquinas térmicas operam de maneira semelhante: recebem calor de uma fonte quente (Qq) e rejeitam parte desse calor, dissipando-o para uma fonte fria (Qf).
Podemos calcular o rendimento de uma máquina térmica qualquer a partir da seguinte fórmula:
Legenda:
η – rendimento da máquina térmica
τ - trabalho da máquina térmica (J)
Qq – calor cedido pela fonte quente (J)
A relação acima pode ser escrita de outra maneira. Para isso, basta assumirmos que o trabalho útil (τ) é dado pela diferença entre a quantidade de calor cedida pela fonte quente (Qq) e a quantidade de calor dissipada para a fonte fria (QF):
Legenda:
QF – calor cedido pela fonte fria (J)
→ Rendimento da máquina de Carnot
O ciclo de Carnot é um ciclo termodinâmico ideal e de maior rendimento possível. Dessa forma, não é possível existir uma máquina térmica operante com as mesmas temperaturas das fontes quente e fria com rendimento maior que o rendimento do ciclo de Carnot.
O rendimento das máquinas baseado no ciclo de Carnot pode ser calculado a partir da fórmula a seguir:
Legenda:
TQ – temperatura da fonte quente (K)
TF – temperatura da fonte fria (K)
Veja também: Máquinas de Carnot
Por Me. Rafael Helerbrock

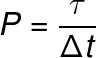
.jpg)