Associação de geradores em série

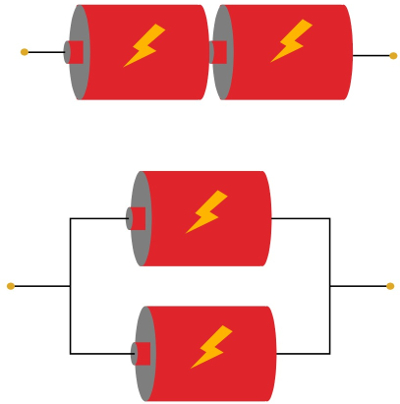
 A associação de geradores elétricos diz respeito à forma como esses dispositivos são ligados à um circuito elétrico. De acordo com a necessidade, é possível associar os geradores em série ou em paralelo. Na associação de geradores em série, somam-se as forças eletromotrizes individuais de cada gerador, bem como as suas resistências elétricas internas, no caso em que esses geradores sejam reais.

Leia também: 5 coisas que você deve saber sobre Eletricidade

Tópicos deste artigo

• 1 - Conceito
• 2 - Fórmulas importantes
• 3 - Resumo
• 4 - Exercícios resolvidos

Conceito

A associação de geradores em série garante que possamos fornecer uma força eletromotriz maior do que somente um gerador seria capaz de ofertar a um circuito elétrico. Por exemplo: se um circuito opera sob a tensão elétrica de 4,5 V, e dispomos somente de pilhas de 1,5 V, é possível conectá-las em série para que apliquemos um potencial de 4,5 V sobre esse circuito.

Um exemplo simples e didático que envolve a associação de geradores em série é o experimento da bateria de limão. Nesse conectamos vários limões em série de modo que o potencial elétrico produzido pelos frutos seja suficientemente grande para ligar uma pequena lâmpada.

Quando associados em série, os limões podem ser usados para acender uma lâmpada.

Na associação de geradores em série, todos os geradores são ligados no mesmo ramo do circuito, e, por esse motivo, todos serão atravessados pela mesma corrente elétrica. A força eletromotriz total oferecida ao circuito é determinada pela soma das forças eletromotrizes de cada um dos geradores.

Apesar de ser muito útil para diversas aplicações, a conexão de geradores reais em série implica um aumento da resistência elétrica do circuito, e, por isso, uma maior quantidade de energia será dissipada em forma de calor, por meio do efeito Joule.

Veja também: A velocidade da corrente elétrica

Fórmulas importantes

De acordo com a equação característica dos geradores, a força eletromotriz (ε) representa toda a energia que um gerador pode produzir. Entretanto, parte dessa energia é dissipada (r.i) pela própria resistência interna dos geradores. Desse modo, a energia que é fornecida pelo circuito é dada pela tensão útil (U):

U_u — Tensão útil (V)

ε — força eletromotriz (V)

r_i — resistência interna (Ω)

i — corrente elétrica (A)

Quando conectamos geradores em série, basta somarmos as suas forças eletromotrizes bem como os potenciais dissipados por suas resistências internas. Fazendo isso, encontramos a lei de Pouillet. De acordo com essa lei, a intensidade da corrente elétrica produzida por uma associação de n geradores pode ser calculada com base na seguinte expressão:

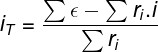
Σε — Soma das forças eletromotrizes (V)

Σr_i — soma das resistências internas dos geradores (Ω)

i_T — corrente total do circuito (A)

Analisando a expressão anterior, podemos perceber que ela permite calcular a corrente elétrica que é formada no circuito. Para tanto, ela relaciona a soma das forças eletromotrizes dividida pela soma das resistências internas. Entretanto, a lei mostrada só é aplicada para a associação de geradores em série, caso haja resistores externos à associação de geradores. A corrente elétrica do circuito pode ser calculada por meio da fórmula a seguir:

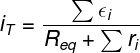
R_eq — Resistência equivalente do circuito (Ω)

Um exemplo dessa situação é mostrado na figura seguinte. Nela temos dois geradores (pilhas) conectados em série que se encontram conectados a duas resistências elétricas (lâmpadas), também ligadas em série.

Na figura temos dois geradores associados em série ligados a duas lâmpadas, também conectadas em série.

Resumo

• Na associação de geradores em série, todos os geradores são ligados no mesmo ramo (fio).

• Nesse tipo de associação, todos os geradores são atravessados pela mesma corrente elétrica.

• Quando conectados em série, a força eletromotriz da associação de geradores é dada pela soma das forças eletromotrizes individuais.

• A resistência equivalente da associação de geradores em série é dada pela soma das resistências individuais.

• Na associação em série, a força eletromotriz fornecida ao circuito aumenta. No entanto, a quantidade de energia dissipada pelo efeito Joule também cresce.

Confira a seguir alguns exercícios resolvidos sobre a associação de geradores em série e entenda mais sobre o assunto.

Veja também: Macetes de fórmulas de Física

Exercícios resolvidos

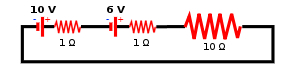
Questão 1) Dois geradores reais, como mostrado na seguinte figura, de forças eletromotrizes iguais a 10 V e 6 V, respectivamente, e resistências internas de 1 Ω cada, são associados em série e ligados a um resistor de 10 Ω. Calcule a corrente elétrica que atravessa esse resistor.

a) 12,5 A

b) 2,50 A

c) 1,33 A

d) 2,67 A

e) 3,45 A

Gabarito: Letra C

Resolução:

Vamos calcular a corrente elétrica total no circuito. Para isso, utilizaremos a lei de Pouillet para geradores conectados em série:

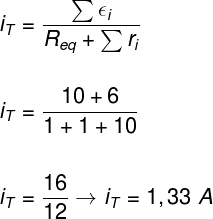
No cálculo feito, somamos as forças eletromotrizes produzidas por cada um dos geradores (10 V e 6 V) e dividimos esse valor pelo módulo da resistência equivalente do circuito (10 Ω) com a soma das resistências internas (1 Ω) dos geradores. Dessa forma, encontramos uma corrente elétrica de 1,33 A.

Questão 2) Três geradores idênticos, de 15 V cada e 0,5 Ω de resistência interna, são ligados em série a um conjunto de 3 resistores de 30 Ω cada, conectados em paralelo entre si. Determine a intensidade da corrente elétrica formada no circuito.

a) 2,8 A

b) 3,9 A

c) 1,7 A

d) 6,1 A

e) 4,6 A

Gabarito: Letra B

Resolução:

Para resolvermos esse exercício, é necessário determinarmos primeiramente o módulo da resistência equivalente dos três resistores externos. Como esses três resistores de 30 Ω estão ligados em paralelo, a resistência equivalente dessa ligação será de 10 Ω:

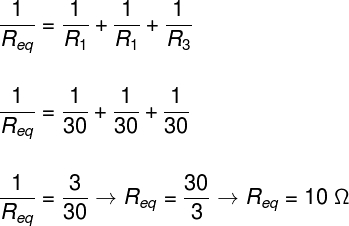
Feito isso, podemos passar para a próxima etapa, na qual somamos os potenciais elétricos de cada gerador e dividimos o resultado pela soma da resistência equivalente e interna:

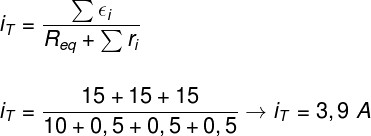
Ao aplicarmos os valores na lei de Pouillet, encontramos uma corrente elétrica de intensidade igual a 3,9 A. Portanto, a alternativa correta é a letra B.

Questão 3) Duas pilhas idênticas de 1,5 V cada e resistência interna de 0,1 Ω são associadas em série a uma lâmpada de resistência igual a 10,0 Ω. A corrente elétrica que atravessa a lâmpada e tensão elétrica entre os seus terminais são, respectivamente, iguais a:

a) 0,350 A e 2,50 V

b) 0,436 A e 4,36 V

c) 0,450 A e 4,50 V

d) 0,300 A e 5,0 V

e) 0,125 A e 1,25 V

Gabarito: Letra B

Resolução:

Por meio da lei de Pouillet, podemos encontrar o módulo da corrente elétrica que passa através da lâmpada, observe:

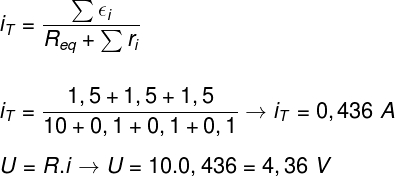
O cálculo feito permite determinarmos que a corrente elétrica que passa através da lâmpada é de 0,436 A e que o potencial elétrico entre os seus terminais é de 4,36 V. O resultado é condizente com o balanço de energias do exercício, uma vez que, juntas, as três pilhas podem fornecer um máximo de 4,5 V.

Por Me. Rafael Helerbrock