Podemos definir uma lente esférica como sendo uma associação de dois dioptros planos em que um deles é necessariamente esférico, enquanto o outro pode ser esférico ou plano. Sendo assim, aqui trataremos como lente esférica qualquer corpo transparente limitado por duas superfícies de um dioptro.
Quanto à nomenclatura das lentes esféricas, temos:
- lentes de bordas finas: biconvexa, plano-convexa e côncavo-convexa
- lentes de bordas espessas: bicôncava, plano-côncava e convexo-côncava.
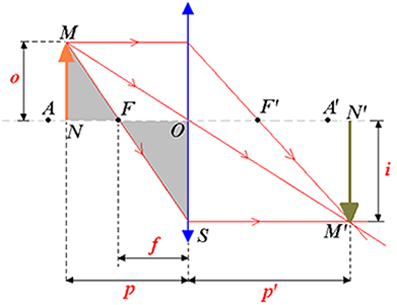
Através de um estudo analítico podemos determinar a altura e a posição de uma imagem conjugada por uma lente esférica. Para isso basta que conheçamos a posição e o tamanho do objeto. Vejamos a figura abaixo:
Vamos supor que temos um objeto MN colocado diante de uma lente esférica convergente. A imagem produzida por essa lente é definida fazendo uso de apenas três raios de luz que saem do objeto. Podemos ver, na figura acima, que a formação da imagem acontece exatamente no ponto de intercessão entre os raios de luz.
Na figura acima temos a figura de dois triângulos (parte pintada). Tomando como bases matemáticas a semelhança de triângulos da figura acima, podemos relacionar as abscissas pe p’, do objeto e da imagem, com distância focal f da lente.
Sendo assim, temos:
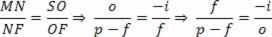
Mas, pela equação do aumento linear,
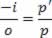
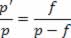
p.p'-p'.f = p.f
p.p' = p'.f+p.f
Multiplicando os dois membros da última expressão por
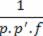
Obtemos:
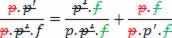
Que resulta em:
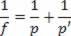
A expressão acima é conhecida como equação dos pontos conjugados ou equação de Gauss.
Por Domiciano Marques
Graduado em Física