Dioptro plano

O dioptro plano é a superfície plana que divide diferentes meios homogêneos e transparentes, fazendo com que observemos a posição aparente do objeto de modo diferente da sua posição real. Isso acontece em razão do fenômeno da refração da luz, no qual a luz muda de meio e sofre mudanças em sua velocidade de propagação, consequentemente alterando a nossa percepção da posição do objeto.

Leia também: Quais são os fenômenos ópticos?

Tópicos deste artigo

• 1 - Resumo sobre o dioptro plano
• 2 - O que é dioptro plano?
• 3 - Fórmula do dioptro plano
• 4 - Como calcular o dioptro plano?
• 5 - Dioptro plano x profundidade aparente
• 6 - Profundidade aparente de uma piscina
• 7 - Exercícios resolvidos sobre dioptro plano

Conceitos básicos de Óptica Geométrica

Saiba mais

Luz

Saiba mais

Resumo sobre o dioptro plano

• O dioptro plano é a superfície plana que divide dois meios transparentes e homogêneos.
• Está relacionado com o fenômeno da refração da luz.
• A fórmula do dioptro plano relaciona os índices de refração dos meios com a distância do objeto e da imagem em relação a uma superfície.
• Dependendo dos índices de refração dos meios, a profundidade aparente do objeto no dioptro plano pode ser menor ou maior do que a profundidade real do objeto no dioptro plano.
• A profundidade aparente de uma piscina é menor do que a profundidade real.

O que é dioptro plano?

O dioptro plano é a superfície plana que separa dois meios transparentes e homogêneos. Caso fosse uma superfície esférica, teriamos um dioptro esférico, e, se fosse uma superfície cilíndrica, teríamos um dioptro cilíndrico.

Ao visualizar um objeto através de um dioptro plano, é possível perceber que a sua imagem está em uma posição diferente (posição aparente) da sua posição real, isso acontece devido ao fenômeno da refração da luz, caracterizado pela mudança de velocidade de propagação da luz quando ela muda de meio.

Quando a luz do objeto sai de um meio de maior índice de refração para um menor (água para ar), a velocidade de propagação da luz aumenta e, consequentemente, os seus raios de luz se afastam da normal (linha imaginária que corta os meios perpendicularmente). Em seguida, esses raios de luz atingem os olhos do observador; contudo, ele não enxerga o “desvio” da luz, ele enxerga o prolongamento dos raios de luz que chegaram a seus olhos, assim, ele visualiza a imagem mais acima (imagem aparente) do que está (imagem real), conforme descrito na imagem abaixo.

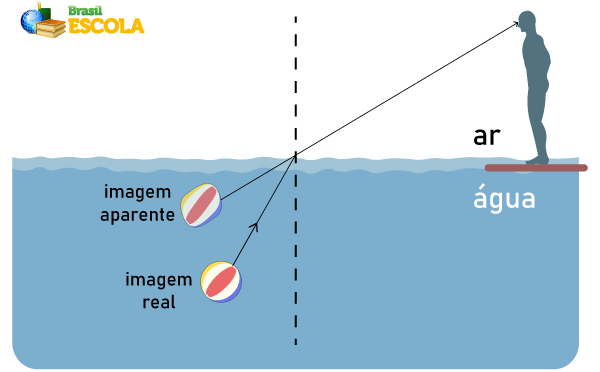
Da mesma forma ocorre quando a luz do objeto sai de um meio de menor índice de refração para um meio de maior refração (ar para água). A velocidade de propagação da luz diminui e, consequentemente, os seus raios de luz se aproximam da normal. Como mencionado anteriormente, o observador visualiza a imagem mais acima do que está, conforme descrito na imagem abaixo.

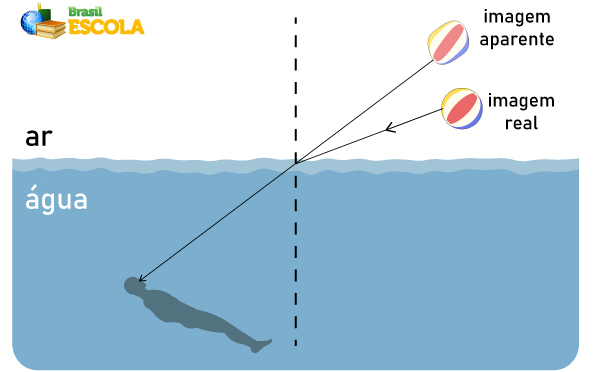
Acesse também: Espelhos planos — superfícies sem qualquer curvatura capazes de promover a reflexão regular da luz

Fórmula do dioptro plano

$\frac{n}{d_o} = \frac{n'}{d_i}$

• n  → índice de refração do objeto que está sendo observado.
• n'  → índice de refração do observador.
• d_o → distância do objeto até a superfície (localização real do objeto).
• d_i  → distância da imagem até a superfície (localização observada do objeto).

Como calcular o dioptro plano?

Sabendo os índices de refração do meio, é possível calcularmos a distância do objeto em relação à superfície ou a distância da imagem em relação à superfície por meio da fórmula do dioptro plano, conforme o exemplo abaixo.

• Exemplo:

Um observador no ar visualiza uma moeda no fundo de uma piscina de 26 cm de profundidade. Com base nessas informações, qual a distância da imagem à superfície.

Resolução:

Calcularemos a distância da imagem à superfície por meio da fórmula do dioptro plano:

$\frac{n}{d_o} = \frac{n'}{d_i}$

$\frac{1,3}{26} = \frac{1}{d_i}$

$d_i=26/1,3$

$d_i=20 cm$

A distância da imagem a superfície é de 20 cm.

Dioptro plano x profundidade aparente

• Profundidade aparente no dioptro plano: é a profundidade em que o observador visualiza o objeto que está em um meio de índice de refração diferente do dele.
• Profundidade real no dioptro plano: é a profundidade exata em que o objeto está.

Em razão do fenômeno da refração, devido aos diferentes índices de refração dos meios, a profundidade aparente pode ser menor ou maior do que a profundidade real.

Profundidade aparente de uma piscina

A profundidade aparente da piscina é menor do que a sua profundidade real, isso acontece devido ao fenômeno da refração. Como o índice de refração do ar é menor que o da água, a luz se propaga com velocidade menor, aproximando o raio de luz da linha normal, assim, o observador de cima visualiza a imagem do fundo da piscina mais em cima do que na realidade ela está. Dessa forma, temos a impressão de que a piscina é mais rasa e só sabemos a sua profundidade real quando entramos nela.

Exercícios resolvidos sobre dioptro plano

Questão 1

(Colégio Naval) Um pescador, em cima de um pequeno barco, observa atento um peixe e estima que ele se encontre a 50 cm de profundidade da superfície de águas calmas da lagoa onde pesca. O que aquele pescador não sabia é que, devido ao fenômeno da refração da luz, neste caso, ao passar de um meio mais refringente (água) para um meio menos refringente (ar atmosférico), a luz sofre uma deflexão, ou, em outras palavras, um desvio em sua trajetória, e temos uma “impressão errada” da profundidade dos objetos. Da mesma forma, quando olhamos para uma piscina com água, estando do lado de fora, temos a sensação de a piscina ser mais rasa. O mesmo fenômeno ocorre quando mergulhamos um lápis em um copo com água e temos a impressão de que o lápis se quebra na superfície da água. Levando-se em consideração o fenômeno da refração da luz ao passar de um meio para outro meio e a partir da estimativa do pescador, calcule a profundidade real a que se encontra o peixe a partir da superfície da lagoa, e assinale a opção correta.

Dados:

Índice de refração do ar atmosférico: 1; e

Índice de refração da água: 1,3.

A) 60 cm   

B) 65 cm   

C) 70 cm   

D) 75 cm   

E) 80 cm 

Resolução:

Alternativa B.

Calcularemos a profundidade real em que se encontra o peixe por meio da fórmula do dioptro plano:

$\frac{n}{d_o} = \frac{n'}{d_i}$

$\frac{n_{\text{água}}}{d_o} = \frac{n'_{\text{ar}}}{d_i}$

$\frac{1,3}{d_o} = \frac{1}{50}$

$d_o=1,3 \cdot 50$

$d_o=65 cm$

Questão 2

(Mackenzie) Certa piscina contém água, de índice de refração absoluto igual a 4/3 e sua base se encontra 3,00 m abaixo da superfície livre. Quando uma pessoa, na beira da piscina, olha perpendicularmente para seu fundo (base), terá a impressão de vê-lo:

Dado: Índice de refração absoluto do ar n = 1

A) 2,25 m mais próximo, em relação à profundidade real.

B) 1,33 m mais próximo, em relação à profundidade real.

C) 0,75 m mais próximo, em relação à profundidade real.

D) 1,33 m mais distante, em relação à profundidade real.

E) 0,75 m mais distante, em relação à profundidade real.

Resolução:

Alternativa C.

Calcularemos a distância da superfície até a imagem por meio da fórmula do dioptro plano:

$\frac{n}{d_o} = \frac{n'}{d'}$

$\frac{n_{\text{água}}}{d_o} = \frac{n'_{\text{ar}}}{d_i}$

$\frac{{4 / 3}}{3} = \frac{1}{d_i}$

$d_i \cdot \frac{4}{3} = 3$

$d_i= 3 \cdot \frac {3}{4}$

$d_i= \frac {9}{4}$

$d_i=2,25 m$

Assim, quando uma pessoa, na beira da piscina, olha perpendicularmente para seu fundo (base), terá a impressão de vê-lo 0,75 m mais próximo em relação à profundidade real.

Fontes

HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Óptica e Física Moderna (vol. 4). 8. ed. Rio de Janeiro, RJ: LTC, 2009.

NUSSENZVEIG, Herch Moysés. Curso de física básica: ótica, relatividade e física quântica (vol. 4). 5 ed. São Paulo: Editora Blucher, 2015.