Efeito Compton

O efeito Compton é um fenômeno descoberto pelo físico Arthur Compton (1892-1962) que faz com que, após a interação dos fótons de raios X ou de raios gama com a matéria, esses fótons desviem-se da trajetória inicial com energia e frequência inferiores às dos raios X ou dos raios gama incidentes no alvo. 

Leia também: O que é o efeito Cherenkov?

Tópicos deste artigo

• 1 - Resumo sobre efeito Compton
• 2 - O que é o efeito Compton?
• 3 - Fórmula da variação de Compton
• 4 - Experimento de Compton
• 5 - Efeito fotoelétrico x efeito Compton
• 6 - Exercícios resolvidos sobre efeito Compton

Resumo sobre efeito Compton

• O efeito Compton é um fenômeno descoberto pelo físico Arthur Compton (1892-1962).
• Devido ao efeito Compton, os raios X ou os raios gama espalhados possuem menor energia e menor frequência do que os raios X ou os raios gama incidentes sobre os alvos.
• O deslocamento de Compton depende apenas do ângulo de espalhamento.
• No experimento Compton, ocorria a interação dos fótons dos raios X incidentes com os elétrons dos alvos de grafite.
• No efeito fotoelétrico, toda a energia dos fótons é transferida para os elétrons da matéria.

O que é o efeito Compton?

Chamado comumentemente de espalhamento de Compton, o efeito Compton é o espalhamento dos fótons de raios X ou de raios gama quando colidem com os elétrons da camada de valência do átomo, diminuindo a energia e a frequência desse fóton e aumentando o seu comprimento de onda.

Fórmula da variação de Compton

\(\Delta \lambda = \frac{h}{m_o \cdot c} \cdot (1 - \cos \theta) \)

• ∆λ  → deslocamento de Compton, medido em metros [m] .
• h  → constante de Planck, que vale aproximadamente 6,63∙10^-34m² ∙ kg/s .
• m_o  → massa de repouso do elétron, que vale 9,11∙10^-31kg .
• c  → velocidade da luz no vácuo, que vale 299.792.458 m/s² .
• \(\frac{h}{m \cdot c} \) → comprimento de onda de Compton do elétron, que vale aproximadamente 2,426 ∙10^-12m ou 0,02426 Å.
• θ  → ângulo  de espalhamento do fóton em relação à direção original.

Nessa fórmula, temos que:

∆λ=λ-λ_o        onde λ>λ_o

• ∆λ  → deslocamento de Compton, medido em metros [m] .
• λ  → comprimento de onda inicial do fóton, medido em metros [m] .
• λ_o  → comprimento de onda do fóton espalhado, medido em metros [m] .

Experimento de Compton

Em 1923, o físico Arthur Compton (1892-1962) realizou o experimento de Compton, que consistiu na emissão de fótons de raios X sobre alvos de grafite, composto de diversos átomos de carbono dotados de elétrons nas suas camadas mais externas, conforme descrito na imagem abaixo:

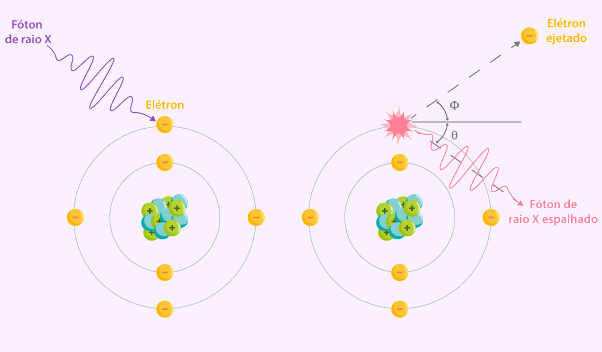
Quando esses fótons colidem com os elétrons do alvo, eles transferem parte da sua energia aos elétrons, os quais, por serem fracamente ligados aos átomos, são ejetados, e o restante da energia dos fótons será desviada para fora da trajetória original com energia menor do que a energia inicial, com menor frequência do que a frequência inicial e, consequentemente, com maior comprimento de onda do que o comprimento inicial. Os elétrons ejetados foram nomeados de “elétrons de Compton”, e os fótons desviados foram nomeados de “radiação secundária ou retroespalhado”.

Efeito fotoelétrico x efeito Compton

O efeito fotoelétrico e o efeito Compton são efeitos que ocorrem através da interação entre os fótons e os elétrons. Enquanto, no efeito Compton, apenas uma parte da energia do fóton é cedida ao elétron, no efeito fotoelétrico, temos a energia do fóton sendo cedida completamente para o elétron, de modo que esse fóton deixa de existir, e a energia do elétron passa a ser a sua energia original mais a energia do fóton. Para saber mais detalhes sobre o efeito fotoelétrico, clique aqui.

Exercícios resolvidos sobre efeito Compton

Questão 1

Calcule o deslocamento de Compton dos raios X quando ele é espalhado com um ângulo θ  igual a 60°. Considere o comprimento de onda de Compton do elétron como 2,43∙10^-12 m .

A) Nulo.

B) 1,002∙10^-12m

C) 1,063∙10^-12m

D) 1,159∙10^-12m

E) 1,215∙10^-12m

Resolução:

Alternativa E.

Calcularemos a deslocamento de Compton através da fórmula do efeito Compton:

\(\Delta \lambda = \frac{h}{m \cdot c} \cdot (1 - \cos \theta) \)

∆λ=2,43∙10^-12∙(1- cos60°)

∆λ=2,43∙10^-12∙(1- 0,5)

∆λ=2,43∙10^-12∙(0,5)

∆λ=1,215∙10^-12 m

Questão 2

(Halliday - Adaptada) Raios X, com λ=1,00 Å , são espalhados por um bloco de carbono. A radiação espalhada é detectada a 90º com a direção do feixe incidente. Qual é o desvio de Compton ∆λ ?

A) 0,0243 Å

B) 0,0365 Å

C) 0,0478 Å

D) 0,0512 Å

E) 0,0695 Å

Resolução:

Alternativa A.

\(\Delta \lambda = \frac{h}{m \cdot c} \cdot (1 - \cos \theta) \)

∆λ=2,43∙10^-12∙(1- cos90°)

∆λ=2,43∙10^-12∙(1- 0 )

∆λ=2,43∙10^-12∙(1)

∆λ=2,43∙10^-12m

∆λ=0,0243 Å

Fontes

HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Ótica e Física Moderna. 8. ed. Rio de Janeiro, RJ: LTC, 2009.

NUSSENZVEIG, Herch Moysés. Curso de física básica: Ótica, Relatividade, Física Quântica (vol. 4). Editora Blucher, 2015.