Tabela verdade

Tabela verdade é um instrumento lógico que contém todos os valores lógicos de uma proposição composta. A construção de uma tabela verdade para uma proposição composta envolve os valores lógicos das proposições simples que a compõem e as operações lógicas entre essas proposições.

Leia também: Afinal, o que é lógica?

Tópicos deste artigo

• 1 - Resumo sobre tabela verdade
• 2 - O que é a tabela verdade?
• 3 - Principais conectivos da tabela verdade
• 4 - Como funciona a tabela verdade?
  • Tabela verdade da negação
  • Tabela verdade da conjunção
  • Tabela verdade da disjunção
  • Tabela verdade da condicional
  • Tabela verdade da bicondicional
• 5 - Construção da tabela verdade
• 6 - Exercícios sobre tabela verdade

Resumo sobre tabela verdade

• Uma tabela verdade é um instrumento empregado na lógica matemática para dispor todos os valores lógicos de uma proposição composta.

• As principais operações lógicas da tabela verdade são negação (~), conjunção (˄), disjunção (˅), condicional (→) e bicondicional (↔).

• Para construir uma tabela verdade de uma proposição composta, é necessário utilizar as tabelas verdade das operações lógicas fundamentais.

O que é a tabela verdade?

Considere p e q proposições simples, ou seja, sentenças às quais podem ser atribuídos um dos seguintes valores lógicos: verdadeiro (V) ou falso (F). Uma proposição composta formada por meio de operações entre p e q também é uma sentença que pode ser verdadeira ou falsa. O valor lógico dessa proposição composta depende dos valores lógicos atribuídos a p e q e à(s) operação(ões) entre elas.

A tabela verdade é uma tabela que apresenta todas as possibilidades de valor lógico para a proposição composta com base nos valores lógicos de p e q.

Neste texto vamos utilizar a letra V para indicar o valor lógico verdadeiro a uma proposição e a letra F para indicar o valor lógico falso.

Principais conectivos da tabela verdade

Os conectivos (ou operadores) lógicos são símbolos ou palavras associados a operações que conectam uma proposição simples com outra proposição simples para produzir uma proposição composta.

Há cinco principais conectivos, cujos operação, símbolo e significado estão indicados no quadro abaixo.

Modo de ler:

• ~ p — “não p”

• p ˄ q — “p e q”

• p ˅ q — “p ou q”

• p→q — “se p então q”

• p↔q — “p se e somente se q”

Observação: A bicondicional é o resultado da operação condicional nos dois sentidos, ou seja, p↔q significa p→q e q→p.

Como funciona a tabela verdade?

Na primeira linha da tabela verdade são indicadas todas as proposições cujos valores lógicos desejamos analisar, além das respectivas operações entre elas. Cada linha da tabela verdade apresenta a relação entre os valores lógicos das proposições da primeira linha.

A fim de construir uma tabela verdade para qualquer proposição composta, é necessário conhecer as tabelas verdades das operações fundamentais, oriundas dos principais conectivos lógicos. Vejamos quais são essas tabelas verdade, obtidas pelas regras do cálculo proposicional.

• Tabela verdade da negação

Dada uma proposição simples p, o valor lógico da proposição ~ p é o contrário do valor lógico de p. Assim, se p é verdadeira, ~ p é falsa; e se p é falsa, ~ p é verdadeira.

• Tabela verdade da conjunção

Dadas as proposições p e q, o valor lógico da proposição p ˄ q é verdadeiro apenas quando ambas as proposições são verdadeiras.

• Tabela verdade da disjunção

Dadas as proposições p e q, o valor lógico da proposição p ˅ q é verdadeiro quando, pelo menos, uma das proposições é verdadeira.

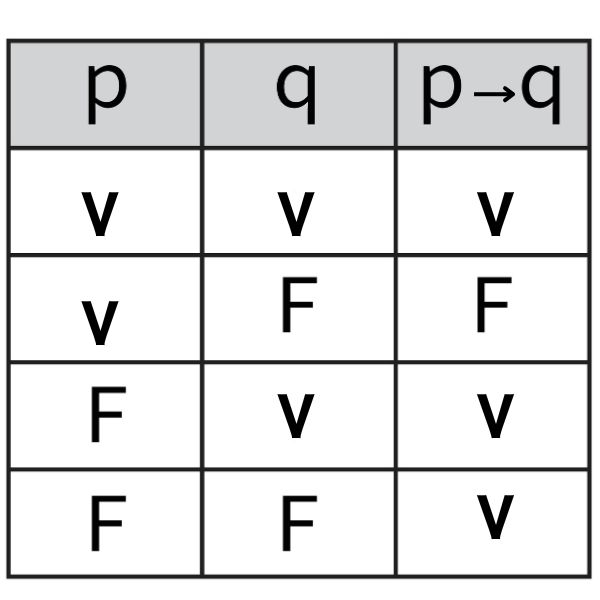
• Tabela verdade da condicional

Dadas as proposições p e q, o valor lógico da proposição p→q é falso quando p é verdadeiro e q é falso e é verdadeiro nos demais casos.

• Tabela verdade da bicondicional

Dadas as proposições p e q, o valor lógico da proposição p↔q é verdadeiro apenas quando ambas as proposições são verdadeiras ou ambas são falsas.

Construção da tabela verdade

Com base nas tabelas verdade das operações fundamentais, podemos construir tabelas verdade para qualquer proposição composta. Para isso devemos identificar as proposições envolvidas e realizar as operações conforme as tabelas verdade do tópico anterior.

Observação: O número de linhas em uma tabela verdade de uma proposição composta formada por n proposições simples é 2ⁿ.

Exemplo: Construa a tabela verdade da proposição ~ (p ˄ q).

Vamos utilizar uma tabela verdade com quatro colunas: uma para a proposição p, uma para a proposição q, uma para a proposição p ˄ q, e a última para a proposição final, que é ~ (p ˄ q).

Podemos preencher as três primeiras colunas dessa tabela com as informações da tabela verdade da operação de conjunção.

Por fim, a quarta coluna é a negação de cada valor lógico da terceira coluna.

Leia também: Como funciona a lógica de Aristóteles

Exercícios sobre tabela verdade

Questão 1

Construa a tabela verdade da proposição ~ (p ˄ ~ q).

Resolução

Vamos utilizar uma tabela verdade com cinco colunas: uma para a proposição p, uma para a proposição q, uma para a proposição ~ q, uma para a proposição p ˄ ~ q, e a última para a proposição final, ~ (p ˄ ~ q).

Agora basta preencher cada coluna e realizar as respectivas operações:

Questão 2

Construa a tabela verdade da proposição ~ p ˅ q → ~ q.

Resolução

Vamos utilizar uma tabela verdade com seis colunas: uma para a proposição p, uma para a proposição q, uma para a proposição ~ p, uma para a proposição ~ q, uma para a proposição ~ p ˅ q, e a última para a proposição final, ~ p ˅ q → ~ q.

Agora basta preencher cada coluna e realizar as respectivas operações:

Fontes

ALENCAR FILHO, E. de. Iniciação à lógica matemática. São Paulo: Nobel, 2002.

VAZ, R. M. Formalização do raciocínio lógico baseada na lógica matemática. Dissertação (Mestrado Profissional em Matemática) – Universidade Federal do Mato Grosso do Sul, Três Lagoas, 2014. Disponível em https://repositorio.ufms.br/handle/123456789/2333 .