Ponte de Wheatstone é um tipo de circuito elétrico que pode ser utilizado para medir, com grande precisão, a resistência elétrica de um resistor desconhecido. Esses circuitos são formados por quatro resistores e um galvanômetro. Dizemos que a ponte de Wheatstone encontra-se em equilíbrio quando não há corrente elétrica fluindo pelo galvanômetro.
O galvanômetro é um dos primeiros dispositivos utilizados para a medida da corrente elétrica. Trata-se de um aparelho de medida que dispõe de uma pequena agulha, usada para indicar a passagem de corrente elétrica por uma bobina que gira, em razão da interação entre a corrente elétrica e o campo magnético produzido por um pequeno ímã.
Leia também: Curiosidades de Física
A figura abaixo mostra o esquema de um galvanômetro. Observe:
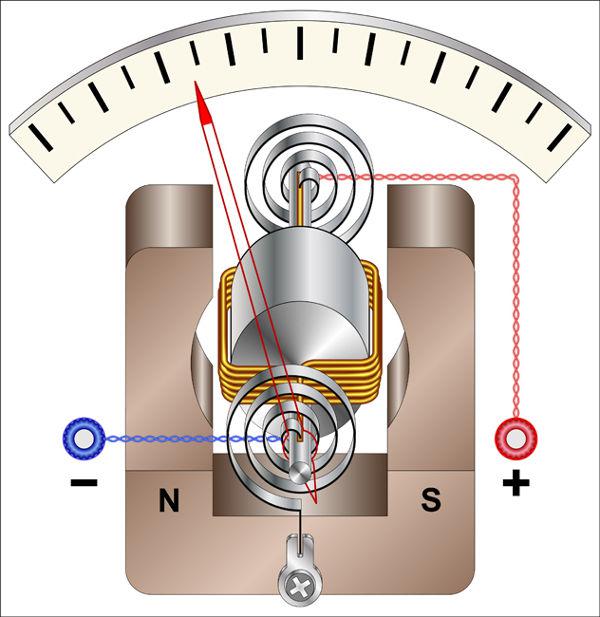
O galvanômetro pode ser usado para medir pequenas correntes elétricas.
Apesar do seu nome, a ponte de Wheatstone foi inventada por Samuel Hunter Christie, no entanto, sofreu grandes modificações e melhorias pelas mãos de Sir Charles Wheatstone, responsável pela popularização desse tipo de circuito. Charles Wheatstone também é conhecido por sua famosa invenção, o reostato – um resistor de resistência variável.
Dos quatro resistores que compõem a ponte de Wheatstone, dois são conhecidos, um pode ser mudado (resistência variável) e um é desconhecido. Conectando uma resistência desconhecida a uma ponte de Wheatstone, deve-se ajustar o valor da resistência variável até que o galvanômetro acuse que não há passagem de corrente elétrica através dele.
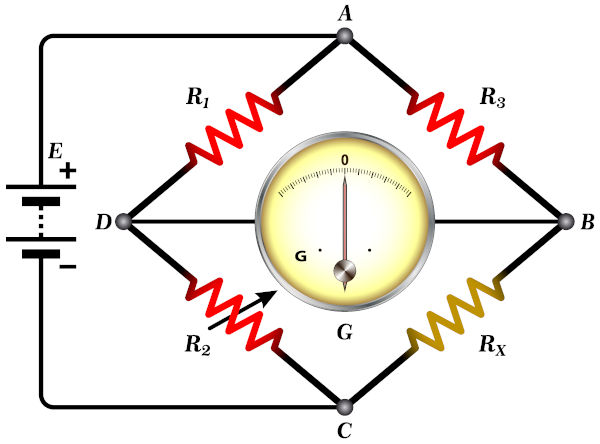
A figura abaixo mostra como é o circuito da ponte de Wheatstone, observe:
.jpg)
ig – corrente no galvanômetro
RX – resistência desconhecida
R1, R2, R3 – resistências conhecidas
Usando o circuito acima, é possível determinar com grande precisão o valor da resistência RX. Para tanto, é necessário que a ponte de Wheatstone esteja em equilíbrio, isso é, a diferenciação de potencial elétrico entre os ramos ACB e ADB deve ser nula, de modo que nenhuma corrente passe pelo galvanômetro do ramo CD.
De acordo com a segunda lei de Kirchhoff, que diz respeito à conservação da energia, sabemos que a soma dos potenciais elétricos em uma malha fechada deve ser nula. Portanto, a soma dos potenciais da malha formado pelos nós ADC e também da malha DBC deve ser igual a 0.
Para calcularmos os potenciais elétricos em cada um desses ramos, usaremos a lei de Ohm, de forma que, em seguida, usando as regras e convenções estabelecidas pelas leis de Kirchhoff e o circuito mostrado na figura anterior, teremos o seguinte resultado:
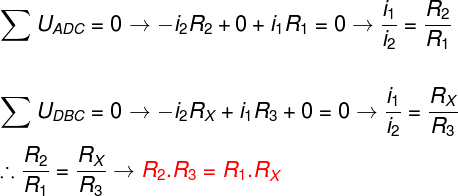
Como consequência da conservação da energia, podemos determinar a resistência desconhecida pelo produto cruzado das resistências.
Após aplicarmos as leis de Kirchoff às malhas citadas anteriormente, concluímos que é possível determinar o módulo da resistência desconhecida por meio do produto cruzado entre as resistências. Outra forma de encontrarmos o mesmo resultado seria admitindo que a queda de potencial entre os pontos A e C e os pontos A e D são iguais, de modo que não haja corrente elétrica fluindo através do galvanômetro.
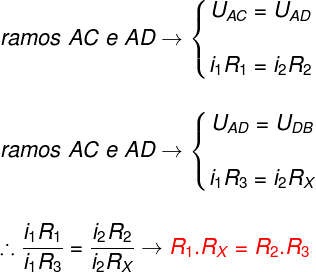
Por meio das quedas de tensão, também é possível encontrar a relação entre os produtos cruzados
Tópicos deste artigo
Videoaula: Ponte de Wheatstone
Aplicações
Além do seu uso comum – medir resistências elétricas desconhecidas, a ponte de Wheatstone também pode ser utilizada em diversos tipos de sensores de precisão como balanças, termostatos, sensores de pressão, sensores de aceleração, detectores de ruídos e movimento etc.
Leia também: Curiosidades sobre eletricidade
Exercícios resolvidos
1) Uma ponte de Wheatstone, como a mostrada na figura abaixo, encontra-se em equilíbrio quando seus três resistores, de resistência 10 Ω, 20 Ω e 30 Ω, são conectados a um quarto resistor de resistência desconhecida.
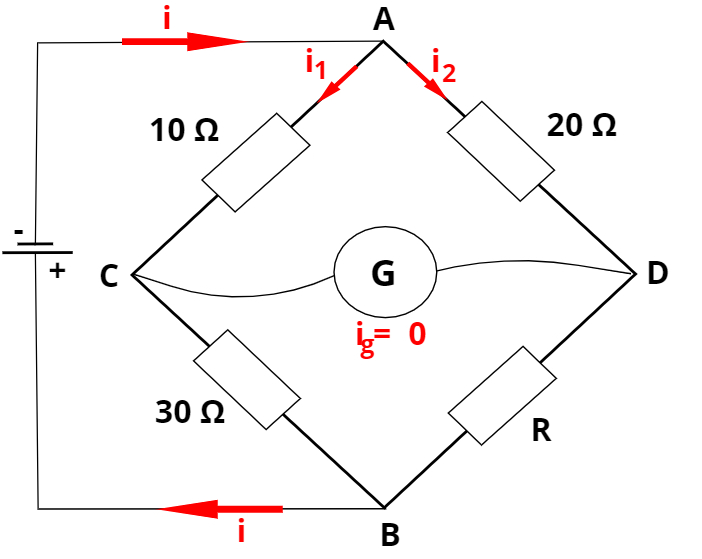
A alternativa que apresenta a resistência elétrica do quarto resistor é:
a) 10 Ω
b) 20 Ω
c) 60 Ω
d) 40 Ω
e) 30 Ω
Resolução:
Gabarito: Letra C
Como a ponte de Wheatstone está em equilíbrio, podemos dizer que o produto cruzado das suas resistências é equivalente. Logo, faremos o seguinte cálculo:
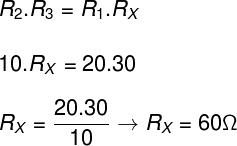
2) Determine o valor da resistência R na ponte de Wheatstone mostrada abaixo. Considere que o circuito encontra-se em equilíbrio.
.jpg)
Resolução:
Como o circuito está em equilíbrio, podemos utilizar o produto cruzado das resistências. Dessa forma, deveremos resolver o seguinte cálculo:
.jpg)
Por Me. Rafael Helerbrock