Força Magnética

A força magnética, ou força de Lorentz, é resultado da interação entre dois corpos dotados de propriedades magnéticas, como ímãs ou cargas elétricas em movimento.

No caso das cargas elétricas, a força magnética passa a existir quando uma partícula eletricamente carregada movimenta-se em uma região onde atua um campo magnético.

Considerando que uma carga pontual Q, com velocidade v, é lançada em uma região onde existe um campo magnético uniforme B, passa a atuar sobre ela uma força magnética com intensidade dada pela seguinte equação:

F = Q.v.B.senα

*α é o ângulo entre os vetores da velocidade v e do campo magnético B.

A direção do campo magnético é perpendicular ao plano que contém os vetores v e F, e o sentido é dado pela regra da mão direita. Observe a figura:

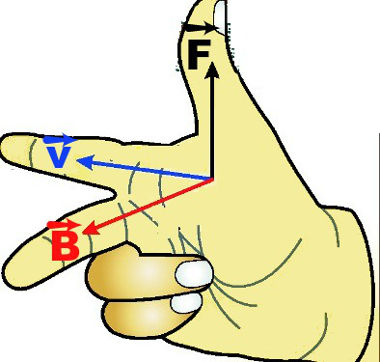
A regra da mão direita mostra o sentido da velocidade, do campo e da força magnética

Veja que o dedo médio aponta na direção do campo magnético B, o indicador indica a direção da vlocidade V com que a carga se movimenta e o polegar aponta no sentido da Força magnética F.

O movimento adquirido pela carga elétrica ao entrar em contato com o campo magnético depende do ângulo em que ela foi lançada:

1. Quando a partícula lançada possui velocidade paralela às linhas de indução do campo magnético, a força magnética é nula.

   Observe que, nesse caso, o ângulo α = 0º ou α = 180 º. A equação que utilizamos para calcular a força é:

   F = Q.v.B.senα.

   E o sen 0º = sen 180º = 0

   Não pare agora... Tem mais depois da publicidade ;)

   Substituindo na equação, teremos:

   F = Q.v.B.0

   F = 0

   Se a força é igual a zero, a partícula mantém-se com a mesma velocidade e realiza movimento retilíneo uniforme na mesma direção do campo magnético.

2. Partícula lançada perpendicularmente ao campo magnético: o ângulo entre v e B será α = 90º. Como sen 90º = 1, teremos:

   F = Q.v.B.sen 90

   F = Q.v.B.1

   F = Q.v.B

   O movimento executado pela partícula é circular e uniforme, e o raio de sua trajetória é obtido da seguinte forma:

   F = F_cp

   Sabemos que:

   F = Q.v.B e F_cp = m.v²
                                    R

   Igualamos as expressões e obtemos:

   Q.v.B = m.v²
                 R

   R = m.v
         Q.B

   Quanto maior for a massa da partícula, maior será o raio de sua trajetória.

3. Partícula lançada obliquamente às linhas de campo: Nesse caso, devemos considerar as componentes x e y do vetor velocidade. A velocidade v_x tem o mesmo sentido que as linhas de campo magnético, enquanto v_y é perpendicular. A resultante da velocidade ocasiona um movimento circular e uniforme, com direção perpendicular ao vetor B, que pode ser denominado de helicoidal uniforme.

A unidade de medida da força magnética é a mesma de qualquer outro tipo de foça: o Newton. Existem inúmeras aplicações da força magnética, dentre elas, podemos citar os seletores de velocidade, motores elétricos e galvanômetros.

Por Mariane Mendes
Graduada em Física