Características da aceleração vetorial

Ao estudarmos alguns conceitos físicos, não devemos nos esquecer de que muitos dos conceitos necessitam ser caracterizados e para isso fazemos uso das unidades de medida. Mas existem alguns conceitos que necessitam de mais características, como, por exemplo, os vetores. As grandezas que precisam ser caracterizadas por um módulo (número acompanhado de uma unidade) e uma orientação espacial são chamadas de grandezas vetoriais.

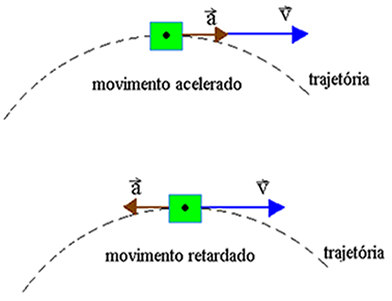
No estudo da aceleração vetorial vimos que ela pode variar em módulo e em direção. Sendo assim, para facilitar a sua análise, a aceleração vetorial em um determinado ponto de uma trajetória é decomposta em duas acelerações componentes: uma denominada aceleração tangencial, relacionada à variação do módulo do vetor velocidade; e outra, normal à trajetória, chamada de aceleração centrípeta, que está relacionada à variação da direção do vetor velocidade.

Características da componente tangencial da aceleração

- a aceleração tangencial mede a rapidez com que o módulo do vetor velocidade varia;
- ela possui módulo igual ao módulo da aceleração escalar;
- a sua direção é sempre tangente à sua trajetória;
- o sentido é o mesmo sentido adotado para o vetor velocidade se o movimento for acelerado; se o movimento for retardado, o sentido é contrário ao vetor velocidade;
- o módulo do vetor aceleração tangencial é nulo nos movimentos uniformes.

Características da componente centrípeta da aceleração

- a componente centrípeta mede a rapidez com que a direção do vetor velocidade varia;
- possui direção radial e aponta sempre para o centro da trajetória;
- possui módulo dado por a_cp = v²/R, em que v é a velocidade instantânea e R é o raio da trajetória descrita pelo móvel;
- nos movimentos retilíneos, a direção do vetor velocidade não varia, portanto a aceleração centrípeta é nula.

Como determinar o vetor aceleração?

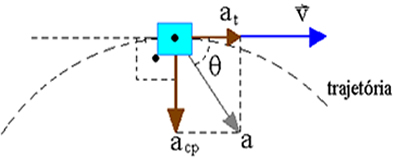
Sabemos que o vetor aceleração tangencial é tangente à trajetória. Ele é orientado no mesmo sentido do movimento e seu módulo é igual ao valor da aceleração escalar.

Pela figura acima podemos determinar o vetor aceleração centrípeta. De acordo com a figura, podemos ver que ele é normal à trajetória, é orientado para o centro da trajetória e seu módulo é dado pela seguinte equação:

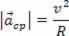
Ainda em relação à figura acima, vemos que as componentes tangencial e centrípeta são ortogonais. Sendo assim, podemos fazer uso do Teorema de Pitágoras para escrever:

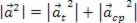
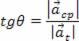
Por Domiciano Marques
Graduado em Física