No estudo da Física, para ficarem bem caracterizadas, existem grandezas cujas medidas precisam da identificação de sua intensidade, de um número acompanhado de uma unidade de medida, e de sua orientação no espaço onde se encontram. Tais grandezas são denominadas grandezas vetoriais. Como exemplo de uma grandeza vetorial há o deslocamento, pois, para descrevê-lo, precisamos da distância percorrida pelo móvel, bem como da sua direção e sentido.
Existem diversas grandezas vetoriais, eis algumas delas: velocidade, deslocamento, posição, quantidade de movimento e aceleração.
Nos nossos estudos relacionados aos movimentos variados, pudemos ver a simples definição da aceleração escalar média. Tal aceleração é definida como sendo o quociente entre a variação da velocidade escalar (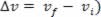
e o respectivo intervalo de tempo (
.
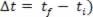De uma maneira parecida, temos a possibilidade de definir a aceleração vetorial média. Vamos considerar que um móvel possua no instante t1 uma velocidade v1 e no instante t2 possua uma velocidade v2. A aceleração vetorial média é assim definida:
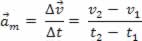
Pela regra do polígono, obtemos o vetor variação de velocidade (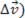
. Vejamos a figura abaixo:
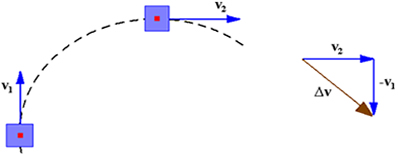
Então, podemos escrever:
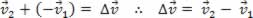
- A aceleração vetorial instantânea (
) pode ser entendida como sendo uma aceleração vetorial média, quando o intervalo de tempo Δt é infinitamente pequeno.
- Sempre que houver variação da velocidade vetorial, 
, haverá aceleração vetorial .
Por Domiciano Marques
Graduado em Física
