Associação de resistores é o circuito elétrico formado por dois ou mais elementos de resistência elétrica ôhmica (constante), ligados em série, paralelo ou ainda, em uma associação mista. Quando ligados em série, os resistores são percorridos pela mesma corrente elétrica, quando em paralelo, o potencial elétrico é igual para os resistores associados.
Veja também: Primeira lei de Ohm: cálculo da resistência elétrica
Tópicos deste artigo
O que são resistores?
Resistores são elementos cuja principal finalidade é a geração de calor mediante a passagem de corrente elétrica. A resistência elétrica, por sua vez, diz respeito à característica dos resistores, que faz com que eles ofereçam resistência à movimentação de cargas em seu interior.

Quando um resistor apresenta resistência elétrica constante, para quaisquer valores de potencial elétrico que for aplicado entre os seus terminais, dizemos que se trata de um resistor ôhmico. Para saber mais sobre esses elementos, leia: resistores.
Resistência equivalente
Resistência equivalente é um recurso utilizado para simplificar circuitos elétricos formados por associações de resistores, ou até mesmo para obtermos resistências elétricas diferentes daquelas que dispomos. Quando calculamos a resistência equivalente buscamos encontrar qual é a resistência de um único resistor que equivale à resistência do conjunto de resistores.
-
Associação de resistores em série
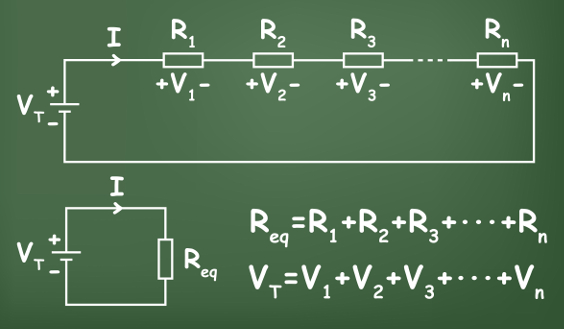
Quando ligados em série, os resistores são percorridos pela mesma corrente elétrica. Na ligação em série, todos os elementos ligados estão conectados no mesmo ramo do circuito, de modo que o terminal de um dos resistores está diretamente ligado ao terminal do próximo resistor. A figura a seguir mostra como é feita uma ligação em série e como essa ligação é representada:

Quando os resistores são ligados em série, o potencial que é aplicado sobre os terminais do circuito é distribuído entre as resistências, em outra palavra, toda a tensão aplicada cai gradativamente ao longo de um circuito que é constituído por resistores em série.
Nesse tipo de ligação, as resistências elétricas individuais somam-se, de modo que a resistência equivalente do circuito é dada pela soma das resistências ligadas em série. Observe:
Resumindo:
-
Na ligação em série, as resistências somam-se,
-
Na ligação em série, os potenciais elétricos somam-se,
-
Na ligação em série, a corrente elétrica é igual para todos os resistores.
A seguir, mostramos a fórmula usada para calcular a resistência equivalente para resistores em série:
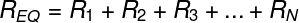
-
Associação em paralelo
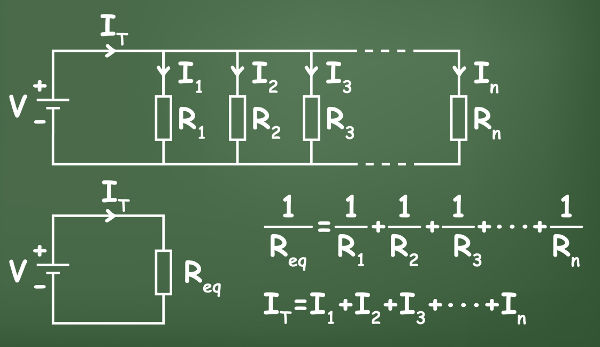
Na associação em paralelo, os resistores encontram-se ligados ao mesmo potencial elétrico, no entanto, a corrente elétrica que atravessa cada resistor pode ser diferente, caso os resistores tenham resistências elétricas diferentes.
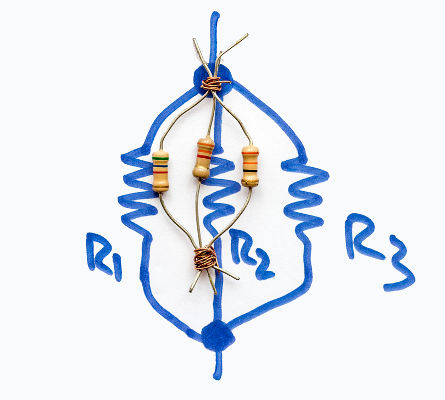
A associação em paralelo é obtida quando os resistores são ligados de modo que a corrente elétrica divide-se ao passar por eles. Nesse tipo de associação, a resistência elétrica equivalente será sempre menor do que a menor das resistências.
Para calcularmos a resistência equivalente na associação de resistores em paralelo, fazemos a soma do inverso das resistências individuais:
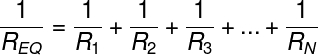
Para o caso em que se deseja calcular a resistência de somente dois resistores em paralelo, é possível fazê-lo por meio do produto pela soma das resistências individuais. Confira:
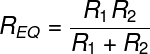
Outro caso específico, é aquele em que N resistores idênticos encontram-se ligados em paralelo. Nesse caso, para calcularmos a resistência equivalente do circuito, basta que se divida o valor da resistência individual pelo número de resistores:
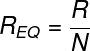
Resumindo:
-
Na ligação em paralelo, a corrente elétrica divide-se de acordo com a resistência elétrica de cada ramo;
-
Na ligação em paralelo, a resistência equivalente é menor que a menor das resistências;
-
Na ligação em paralelo, todos os resistores encontram-se ligados sob o mesmo potencial elétrico.
-
Associação mista de resistores
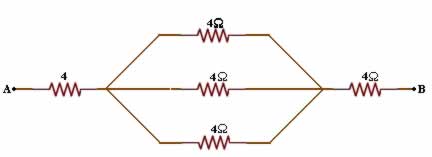
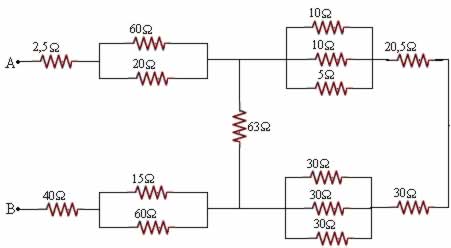
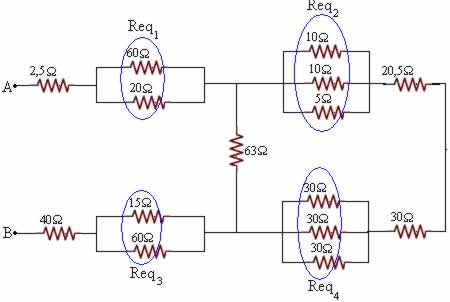
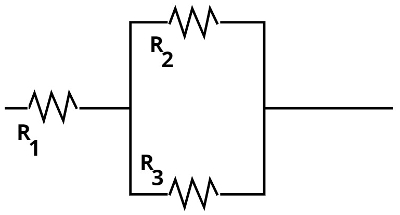
Na associação mista de resistores, pode haver tanto ligações em série quanto ligações em paralelo. Observe a figura a seguir, é possível ver diversos resistores ligados em série, conectados a dois resistores que estão ligados em paralelo entre si:

Para solucioná-la, é necessário que se resolva separadamente, os resistores que encontram-se ligados em paralelo e os resistores que encontram-se ligados em série.
-
Quando houver resistores em série fora da ligação em paralelo, é possível resolver a associação em paralelo para, em seguida, somarmos o resultado obtido à resistência dos demais resistores ligados em série;
-
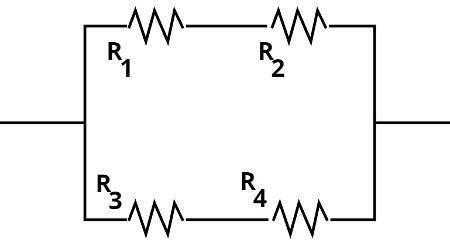
Quando houver resistores ligados em série dentro de uma ligação em paralelo, é necessário que se some as resistências para que, em seguida, realizemos o cálculo da resistência equivalente em paralelo.
Veja também: Geradores elétricos: o que são e como calcular a força eletromotriz
Exercícios resolvidos
Questão 1) Quatro resistores ôhmicos de resistências iguais a 10 Ω, 20 Ω, 30 Ω e 40 Ω são ligados em série e depois em paralelo. Os valores obtidos para a resistência equivalente em cada um desses casos, são, respectivamente, iguais a:
a) 150 Ω e 36 Ω
b) 10 Ω e 92 Ω
c) 100 Ω e 4,8 Ω
d) 15 Ω e 12 Ω
e) 30 Ω e 90 Ω
Resolução
Alternativa c. Para calcularmos a resistência equivalente em série, basta somarmos cada uma das resistências, desse modo, a resistência equivalente da associação em série será de 100 Ω. Para que calculemos a resistência equivalente desse conjunto de resistores, quando associados em paralelo, devemos fazer o seguinte cálculo, observe:
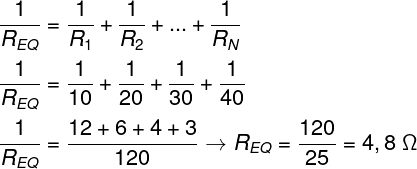
Para fazermos o cálculo apresentado, foi necessário que calculássemos o mínimo múltiplo comum entre os numeradores 10, 20, 30 e 40. Em seguida, fizemos a multiplicação cruzada, resultando em uma resistência equivalente menor que a menor das resistências e igual a aproximadamente 4,8 Ω.
Questão 2) Calcule a resistência equivalente aproximada de uma associação mista em que dois resistores, de 10 Ω e 20 Ω, encontram-se associados em série a outros dois resistores, de 30 Ω e 40 Ω, associados em paralelo.
a) 80 Ω
b) 47 Ω
c) 33 Ω
d) 51 Ω
e) 27 Ω
Resolução:
Alternativa b. Primeiramente, somamos as resistências de 10 Ω e 20 Ω, resultando em 30 Ω. Em seguida, fazemos o produto pela soma entre as resistências de 30 Ω e 40 Ω, resultando em 120/7 Ω, aproximadamente 17,1 Ω. A soma dessas resistências equivalentes é, portanto, aproximadamente 47 Ω.