A resolução de equações é uma atividade cotidiana. Intuitivamente resolvemos equações em nosso dia a dia e nem nos damos conta disso. Ao fazer o seguinte questionamento: “A que horas deverei levantar para ir à escola de forma que não chegue atrasado?” e obtemos a resposta, na verdade acabamos de resolver uma equação onde a incógnita é o tempo. Essas questões cotidianas sempre instigaram matemáticos de todas as épocas na busca de soluções e métodos de resoluções de equações.
A fórmula de Báskara é um dos mais famosos métodos de resolução de uma equação. Trata-se de uma “receita”, um modelo matemático que fornece, quase que instantaneamente, as raízes de uma equação do 2º grau. O interessante é que não existem tantas fórmulas para resolução de equações como se imagina. Equações do terceiro e quarto graus são muito complicadas de se resolver, havendo fórmulas de resolução para os casos mais simples desses tipos de equações.
É interessante saber que o grau da equação é que determina quantas raízes ela apresenta. Sabemos que uma equação do 2º grau apresenta duas raízes. Logo, uma equação do 3º grau terá três raízes e, assim, sucessivamente. Agora, vamos observar o que ocorre com algumas equações.
Exemplo. Resolva as equações:
a) x2 + 3x – 4 = 0
Solução: Aplicando a fórmula de Báskara para resolução de uma equação do 2º grau, obtemos:
![]()
Sabemos que a = 1, b= 3 e c = – 4. Assim,
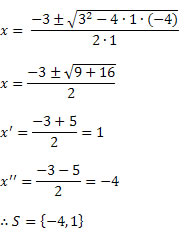
Como resolvemos uma equação do 2º grau, temos duas raízes.
b) x3 – 8 = 0
Solução: Nesse caso, temos uma equação do terceiro grau incompleta de simples resolução.
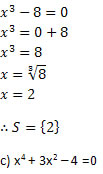
Solução: Nesse caso, temos uma equação do 4º grau incompleta, também chamada de equação biquadrada. A solução desse tipo de equação também é simples. Veja:
A equação x4 + 3x2 – 4 = 0 pode ser reescrita da seguinte forma:
(x2)2 + 3x2 – 4 =0
Fazendo x2 = t e substituindo na equação acima obtemos:
t2 + 3t – 4 = 0 → que é uma equação do 2º grau.
Podemos resolver essa equação utilizando a fórmula de Báskara.
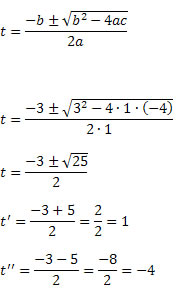
Esses valores não são as raízes da equação, pois a incógnita é x e não t. Mas temos que:
x2 = t
Então,
x2 = 1 ou x2 = – 4
De x2 = 1, obtemos que x = 1 ou x = – 1.
De x2 = – 4, obtemos que não há números reais que satisfaçam a equação.
Portanto, S = {– 1, 1}
Observe que na alternativa a tínhamos uma equação de 2º grau e encontramos duas raízes. Na alternativa b resolvemos uma equação do 3º grau e encontramos apenas uma raiz. E a equação do item c, tratava-se de uma equação do 4º grau e encontramos apenas duas raízes.
Como foi dito anteriormente, o grau da equação determina quantas raízes ela possui:
Grau 2 → duas raízes
Grau 3 → três raízes
Grau 4 → quatro raízes
Mas o que ocorreu com as equações das alternativas b e c?
Acontece que uma equação de grau n ≥ 2 pode ter raízes reais e raízes complexas. No caso da equação de terceiro grau do item b encontramos apenas uma raiz real, as outras duas raízes são números complexos. O mesmo ocorre para a equação do item c: encontramos duas raízes reais, as outras duas são complexas.
Sobre raízes complexas, temos o seguinte Teorema.
Se o número complexo a + bi, b ≠ 0, for raiz da equação a0xn + a1xn-1+ ... + an-1x + an = 0, de coeficientes reais, então seu conjugado, a – bi, também é raiz da equação.
São consequências do Teorema:
• Equação do 2º grau com coeficientes reais → apresenta apenas raízes reais ou duas raízes complexas conjugadas.
• Equação do 3º grau com coeficientes reais → possui somente raízes reais ou uma raiz real e duas raízes complexas conjugadas.
• Equação do 4º grau com coeficientes reais → apresenta apenas raízes reais ou duas raízes complexas conjugadas e duas reais ou somente quatro raízes complexas conjugadas, duas a duas.
• Equação do 5º grau com coeficientes reais → tem apenas raízes reais ou duas raízes complexas conjugadas e as outras reais ou pelo menos uma raiz real e as outras raízes complexas, duas a duas conjugadas.
O mesmo ocorre para equações de graus superiores a 5.
Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática
Equipe Brasil Escola