No estudo da Óptica vimos que refração é o nome dado ao fenômeno que ocorre quando a luz, ao passar de um meio para outro, sofre uma variação em sua velocidade de propagação. No estudo da refração vimos as duas leis que regem esse fenômeno. A primeira delas diz que o raio incidente, a reta N, normal à superfície de separação no ponto de incidência, e o raio refratado são coplanares, ou seja, eles estão no mesmo plano.
Já a segunda lei da refração, também conhecida como Lei de Snell-Descartes, diz que, na refração, o produto do índice de refração do meio (no qual se encontra o raio pelo seno do ângulo que esse raio forma com a reta normal à interface no ponto de incidência) é constante. Dessa forma, é possível escrever que:
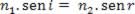
Cabe ressaltar que, quando um raio de luz passa de um meio para outro menos refringente, o raio de luz refrata-se, afastando-se da reta normal perpendicular à superfície. Dessa forma, pode-se observar que, a partir de determinado ângulo de incidência, não há mais refração. Esse ângulo é denominado ângulo limite ou ângulo crítico.
Cálculo do ângulo limite
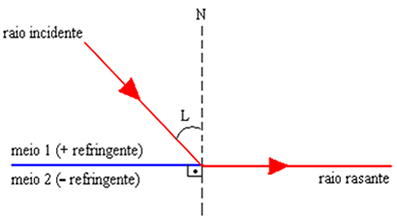
De acordo com a figura acima, a aplicação da Lei de Snell-Descartes à situação nos permite calcular o seno do ângulo limite L através da seguinte relação:
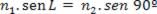
Como sen 90º = 1, temos:
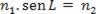
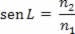
De acordo com a equação acima, podemos ver que o seno do ângulo limite é o quociente entre o índice de refração do meio menos refringente pelo índice de refração do meio mais refringente, isto é:
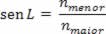
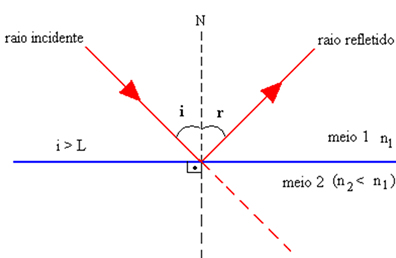
Na figura abaixo podemos ver que quando i > L, não ocorre refração. Sendo assim, os raios são todos refletidos e o fenômeno passa a ser chamado de reflexão total interna.
Por Domiciano Marques
Graduado em Física
