Aceleração vetorial média

No estudo da Física, para ficarem bem caracterizadas, existem grandezas cujas medidas precisam da identificação de sua intensidade, de um número acompanhado de uma unidade de medida, e de sua orientação no espaço onde se encontram. Tais grandezas são denominadas grandezas vetoriais. Como exemplo de uma grandeza vetorial há o deslocamento, pois, para descrevê-lo, precisamos da distância percorrida pelo móvel, bem como da sua direção e sentido.

Existem diversas grandezas vetoriais, eis algumas delas: velocidade, deslocamento, posição, quantidade de movimento e aceleração.

Nos nossos estudos relacionados aos movimentos variados, pudemos ver a simples definição da aceleração escalar média. Tal aceleração é definida como sendo o quociente entre a variação da velocidade escalar (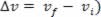 e o respectivo intervalo de tempo (.

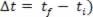De uma maneira parecida, temos a possibilidade de definir a aceleração vetorial média. Vamos considerar que um móvel possua no instante t₁ uma velocidade v₁ e no instante t₂ possua uma velocidade v₂. A aceleração vetorial média é assim definida:

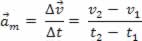
Pela regra do polígono, obtemos o vetor variação de velocidade (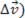. Vejamos a figura abaixo:

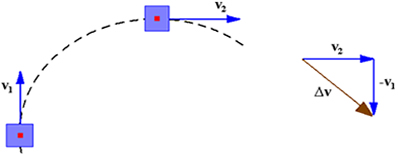
Então, podemos escrever:

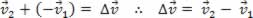
- A aceleração vetorial instantânea () pode ser entendida como sendo uma aceleração vetorial média, quando o intervalo de tempo Δt é infinitamente pequeno.
- Sempre que houver variação da velocidade vetorial, , haverá aceleração vetorial .

Por Domiciano Marques
Graduado em Física